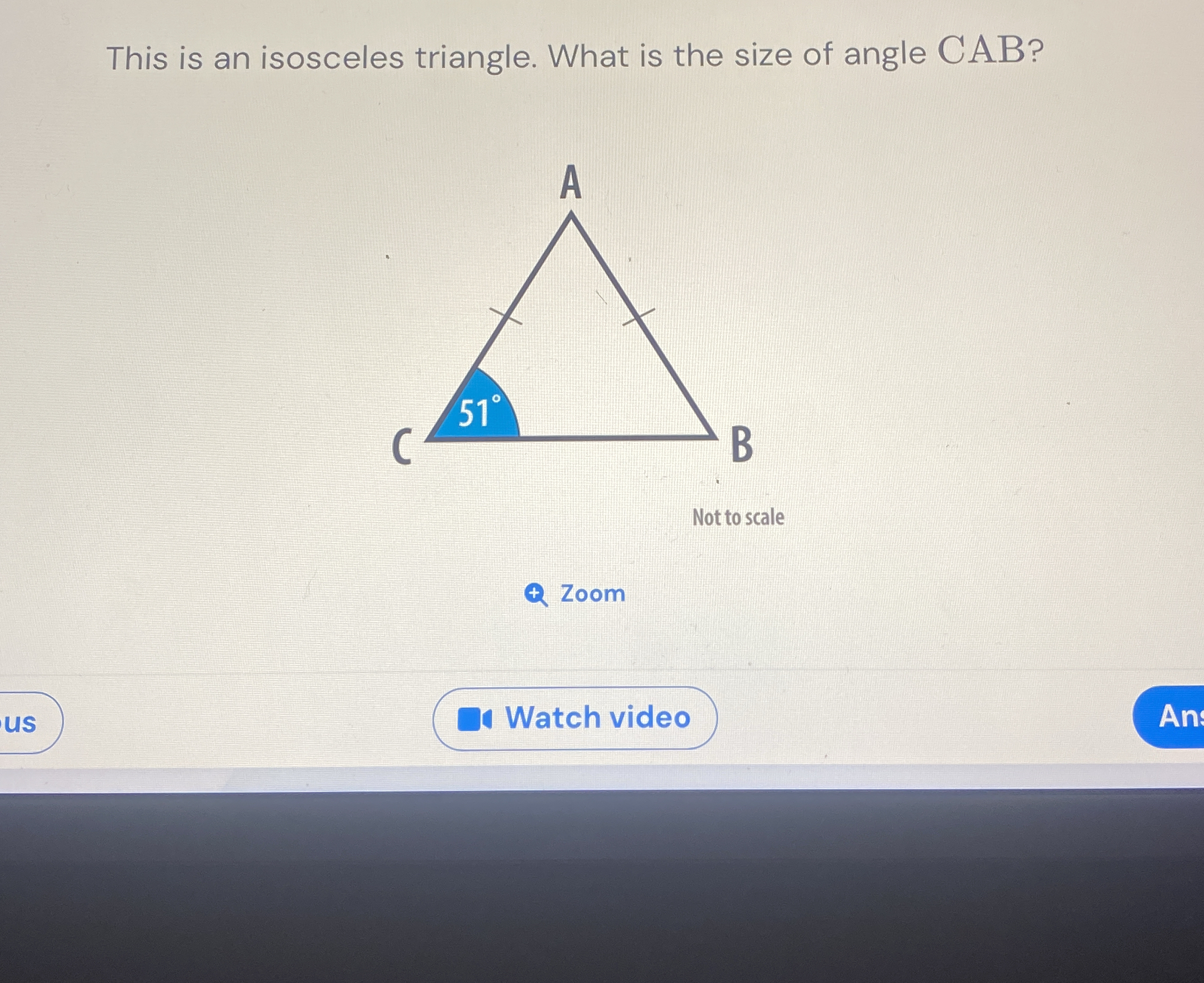
This is an isosceles triangle. What is the size of angle CAB?
Understand the Problem
The question is asking for the size of angle CAB in an isosceles triangle where angle C is given as 51°. In an isosceles triangle, the two angles opposite the equal sides are equal. Therefore, the solution involves finding the measures of the other angles using the fact that the sum of angles in a triangle is 180°.
Answer
The size of angle CAB is $64.5^\circ$.
Answer for screen readers
The measure of angle CAB is $64.5^\circ$.
Steps to Solve
- Identify the properties of an isosceles triangle
An isosceles triangle has two equal angles opposite the equal sides. In this case, let's denote angle CAB as $x$ and angle ABC as $x$ as well.
- Use the triangle angle sum property
The sum of the angles in any triangle is always $180^\circ$. Therefore, we can set up the equation:
$$ x + x + 51^\circ = 180^\circ $$
This simplifies to:
$$ 2x + 51^\circ = 180^\circ $$
- Isolate the variable
Now, we will isolate $x$ by subtracting $51^\circ$ from both sides:
$$ 2x = 180^\circ - 51^\circ $$
Calculating the right-hand side:
$$ 2x = 129^\circ $$
- Solve for x
Now, divide both sides by 2 to find the value of $x$:
$$ x = \frac{129^\circ}{2} = 64.5^\circ $$
Thus, the size of angle CAB is $64.5^\circ$.
The measure of angle CAB is $64.5^\circ$.
More Information
In any triangle, the sum of the internal angles equals $180^\circ$. Isosceles triangles feature two equal angles, making them a unique case in geometry.
Tips
- Confusing the angles: It's important to represent the correct angles—ensure you label them correctly in reaching the solution.
- Forgetting the triangle sum rule: Always remember to sum all angles to $180^\circ$ when dealing with triangles.
AI-generated content may contain errors. Please verify critical information