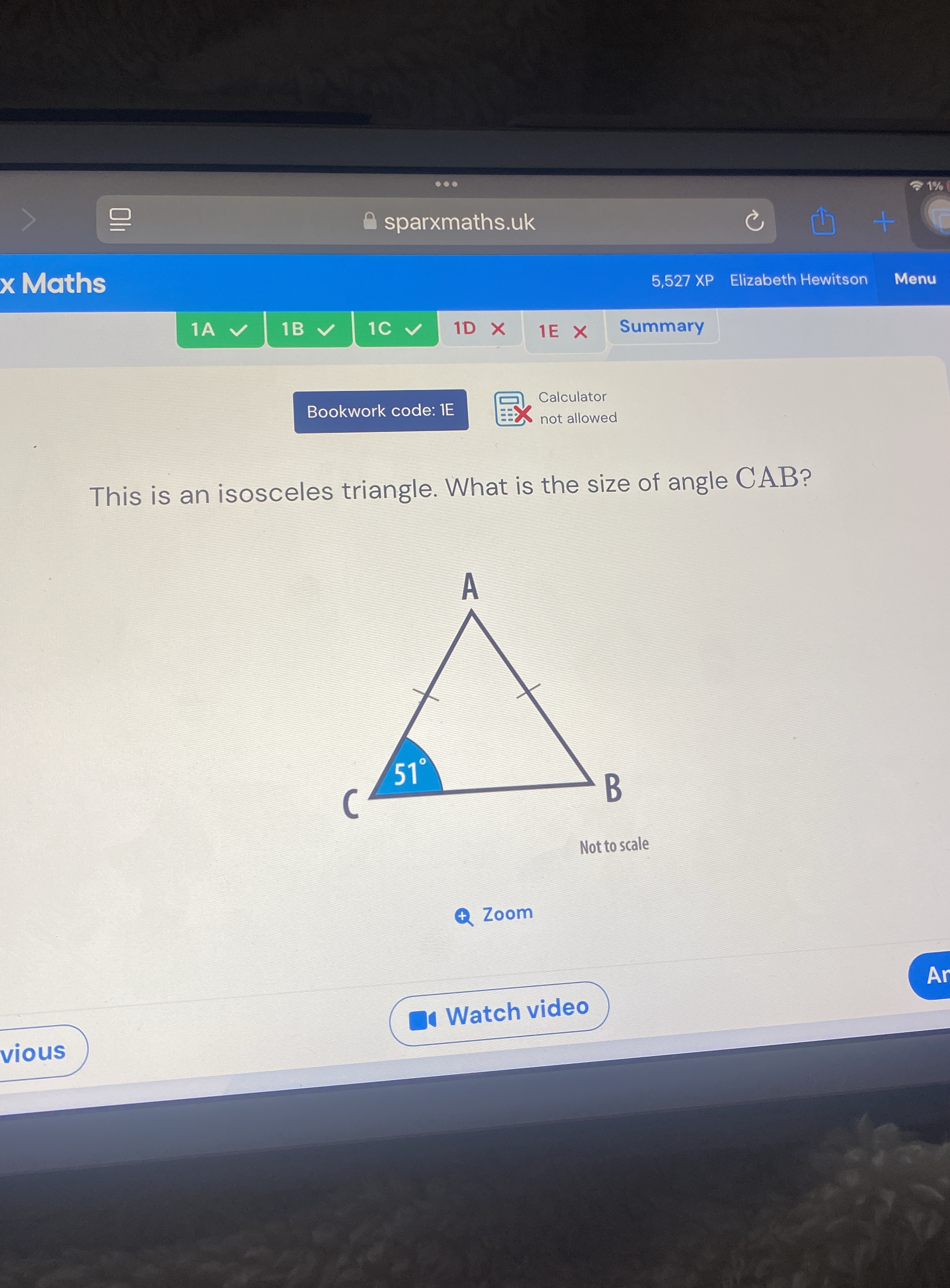
This is an isosceles triangle. What is the size of angle CAB?
Understand the Problem
The question is asking for the measurement of angle CAB in an isosceles triangle where one of the angles, angle C, is given as 51 degrees. Since it's an isosceles triangle, the two angles opposite the equal sides are the same. We need to find the value of angle CAB using the properties of triangles.
Answer
The measure of angle CAB is $64.5$ degrees.
Answer for screen readers
The size of angle CAB is $64.5$ degrees.
Steps to Solve
- Understanding the triangle's properties
In an isosceles triangle, two angles are equal. Given that angle $C$ measures 51 degrees, the triangle has two equal angles which will be angles $A$ and $B$.
- Using the triangle sum property
The sum of the internal angles in any triangle equals 180 degrees. Therefore, we can express this relationship as: $$ A + B + C = 180 $$
- Substituting known values
Knowing angles $A$ and $B$ are equal, we can say: $$ A + A + 51 = 180 $$
- Simplifying the equation
This simplifies to: $$ 2A + 51 = 180 $$
- Solving for angle A
Subtract 51 from both sides: $$ 2A = 180 - 51 $$
Calculating the right side gives: $$ 2A = 129 $$
Now, divide both sides by 2 to solve for $A$: $$ A = \frac{129}{2} = 64.5 $$
Thus, angle $CAB$ measures 64.5 degrees.
The size of angle CAB is $64.5$ degrees.
More Information
In an isosceles triangle, the two equal angles correspond to the sides that are equal in length. Here, we found that since angle C is given as 51 degrees, the two equal angles measure 64.5 degrees each.
Tips
- Forgetting to account for that the triangle's angles sum to 180 degrees can lead to incorrect conclusions.
- Assuming angles A and B have different measures without recognizing the properties of isosceles triangles.
AI-generated content may contain errors. Please verify critical information