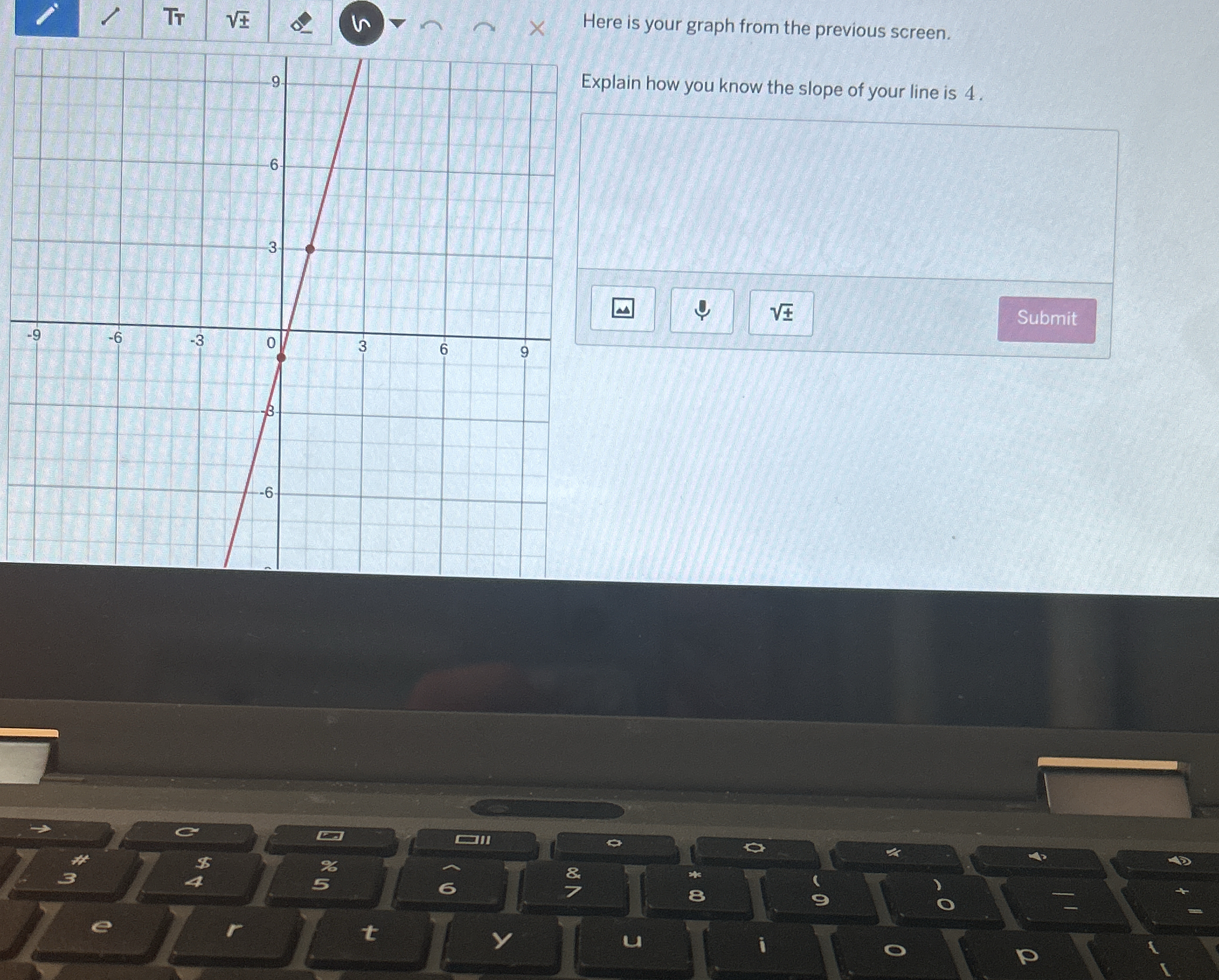
Explain how you know the slope of your line is 4.
Understand the Problem
The question is asking the user to explain how they determined that the slope of their line is 4, which involves understanding the concept of slope in graphing.
Answer
The slope of the line is $4$.
Answer for screen readers
The slope of the line is $4$.
Steps to Solve
- Understanding Slope Definition
The slope of a line measures its steepness and direction. It is calculated using the formula: $$ m = \frac{\Delta y}{\Delta x} $$ where $\Delta y$ is the change in the y-values, and $\Delta x$ is the change in the x-values between two points on the line.
- Identifying Points on the Line
To find the slope, select two clear points on the line. Let's say the points are ( (x_1, y_1) ) and ( (x_2, y_2) ). For instance, mark points at coordinates like ( (0, 8) ) and ( (1, 12) ).
- Calculating Changes in Coordinates
Identify the differences in the coordinates: $$ \Delta y = y_2 - y_1 $$ $$ \Delta x = x_2 - x_1 $$ For our points ( (0, 8) ) and ( (1, 12) ): $$ \Delta y = 12 - 8 = 4 $$ $$ \Delta x = 1 - 0 = 1 $$
- Finding the Slope
Now plug the changes into the slope formula: $$ m = \frac{\Delta y}{\Delta x} = \frac{4}{1} = 4 $$
Thus, this confirms that the slope of the line is indeed 4.
The slope of the line is $4$.
More Information
The slope indicates that for every 1 unit the line moves horizontally, it rises 4 units vertically. This is characteristic of linear relationships in algebra.
Tips
- Choosing Incorrect Points: Ensure that the two points chosen are accurate and clearly lie on the line.
- Miscalculating Differences: Carefully check the subtraction for $y$ and $x$ values to avoid errors in calculating $\Delta y$ and $\Delta x$.
AI-generated content may contain errors. Please verify critical information