The weight limit on an elevator is 2000 pounds. Write and graph an inequality that represents the numbers of large (x) and small (y) boxes. Identify the graph of an inequality.

Steps to Solve

1. Identify the weights of large and small boxes

From the problem, we know:

• 2 large boxes weigh 270 pounds, so the weight of 1 large box is $\frac{270}{2} = 135$ pounds.
• 3 small boxes weigh 270 pounds, so the weight of 1 small box is $\frac{270}{3} = 90$ pounds.
• 1 large box and 4 small boxes weigh 235 pounds, which is helpful to affirm calculations.

2. Set up the inequality

Let:

• $x$ = number of large boxes
• $y$ = number of small boxes

The weight limit for the elevator is 2000 pounds. The inequality can be set up as: $$ 135x + 90y + 200 \leq 2000 $$

3. Simplify the inequality

Subtract 200 from both sides: $$ 135x + 90y \leq 1800 $$

4. Rearrange the inequality

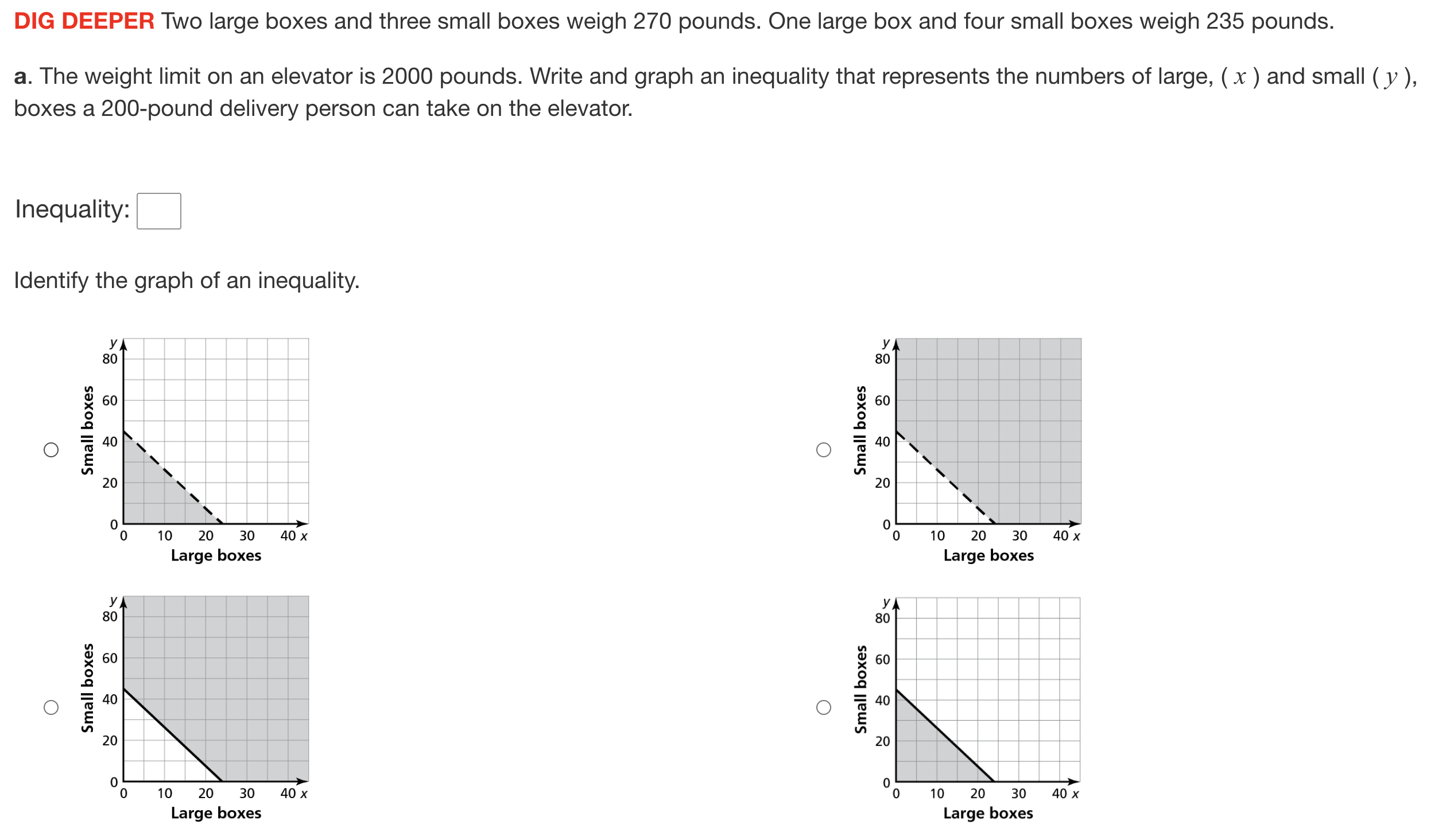
To graph the inequality, express it in slope-intercept form ($y = mx + b$): $$ 90y \leq -135x + 1800 $$ Dividing everything by 90 gives: $$ y \leq -\frac{135}{90}x + 20 $$ which simplifies further to: $$ y \leq -1.5x + 20 $$

5. Graph the inequality

• The line $y = -1.5x + 20$ is a decreasing line.
• Since the inequality is less than or equal to ($\leq$), the area below this line, including the line itself, is the solution region.