(2x^0y^2)^{-3} · 2yx^3
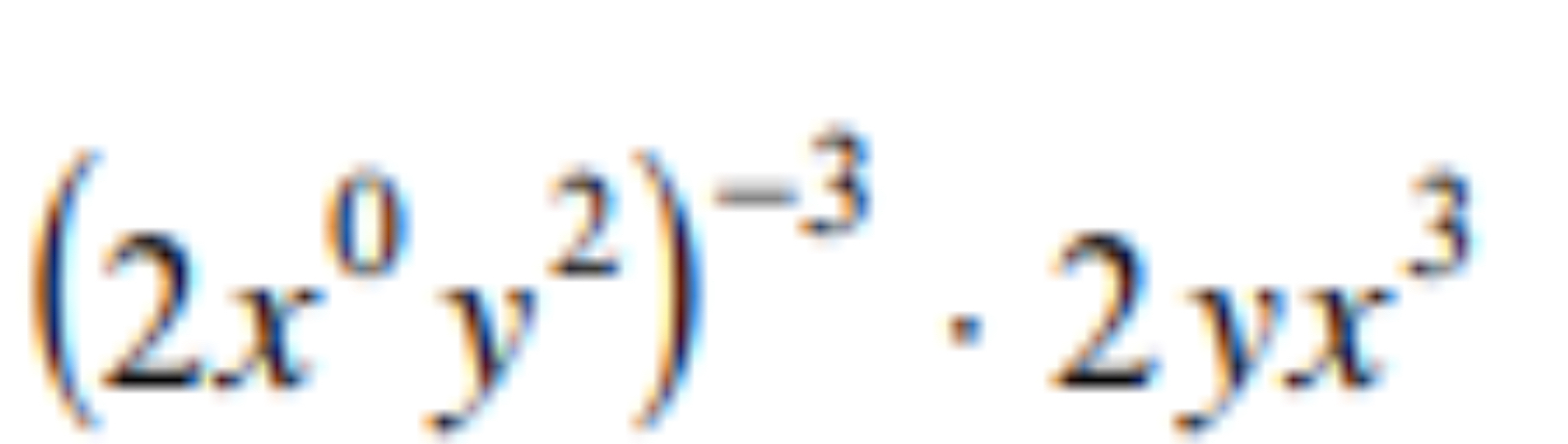
Understand the Problem
The question is asking for the simplification of a mathematical expression involving exponents and multiplication. We need to apply the rules of exponents to simplify the expression correctly.
Answer
The simplified expression is $\frac{x^3}{4y^5}$.
Answer for screen readers
The simplified expression is: $$ \frac{x^3}{4y^5} $$
Steps to Solve
-
Simplify the first expression We begin with the expression $(2x^0y^2)^{-3}$. Recall that $x^0 = 1$ for any $x$. Therefore, we can simplify it to: $$ (2 \cdot 1 \cdot y^2)^{-3} = (2y^2)^{-3} $$
-
Apply the negative exponent rule The negative exponent rule states that $a^{-n} = \frac{1}{a^n}$. Applying this, we have: $$ (2y^2)^{-3} = \frac{1}{(2y^2)^3} $$
-
Calculate $(2y^2)^3$ Using the property of exponents $(ab)^n = a^n b^n$, we get: $$ (2y^2)^3 = 2^3(y^2)^3 = 8y^6 $$
-
Combine the two expressions Now substitute the simplified expression back into the original problem: $$ \frac{1}{8y^6} \cdot 2yx^3 $$
-
Multiply the fractions Combining the fractions, we get: $$ \frac{2yx^3}{8y^6} = \frac{2x^3}{8y^5} = \frac{x^3}{4y^5} $$
The simplified expression is: $$ \frac{x^3}{4y^5} $$
More Information
This expression shows that we have simplified the initial problem significantly by applying the rules for exponents and basic multiplication principles. It's important to remember the negative exponent rule and how to handle expressions within parentheses.
Tips
- Ignoring the value of $x^0$: Remember that $x^0$ equals 1.
- Misapplying the power of a product: Be careful when using $(ab)^n$; remember to apply the exponent to each factor.
AI-generated content may contain errors. Please verify critical information