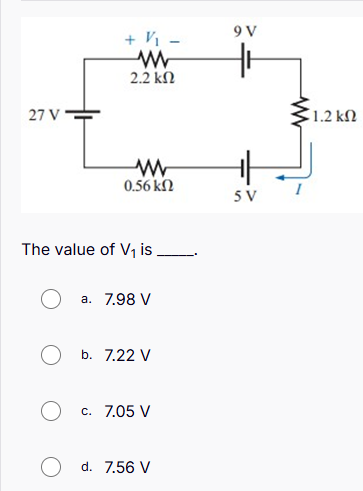
The value of V1 is ____.

Steps to Solve

1. Identify Circuit Components

The circuit consists of a 27 V source, two resistors (2.2 kΩ and 1.2 kΩ), a 0.56 kΩ resistor, and voltage sources of 9 V and 5 V. The goal is to find the voltage $V_1$ across the 2.2 kΩ resistor.

2. Apply Kirchhoff's Voltage Law

According to Kirchhoff's Voltage Law, the sum of the voltage around the loop should equal zero:

$$ -27 + V_1 + 9 + 5 + I(2.2 \text{ kΩ}) + I(1.2 \text{ kΩ}) = 0 $$

3. Calculate Total Current Using Resistors

Combine the resistances in the current path: The total resistance ($R_t$) of the resistors in series ($0.56 \text{kΩ} + 1.2 \text{kΩ}$) is:

$$ R_t = 0.56 + 1.2 = 1.76 \text{ kΩ} $$

Using Ohm's Law ($V = IR$), the current $I$ in the circuit can be calculated as:

$$ I = \frac{27 - 9 - 5}{1.76} = \frac{13}{1.76 \text{ kΩ}} \approx 7.39 \text{ mA} $$

4. Calculate Voltage Across the 2.2 kΩ Resistor

Now use the current $I$ to find $V_1$:

$$ V_1 = I \cdot 2.2 \text{ kΩ} \approx (7.39 \text{ mA})(2.2 \text{ kΩ}) $$

5. Solve for Voltage across the Resistor

Convert current to amps:

$$ I = 0.00739 \text{ A} $$

Now substituting gives:

$$ V_1 = 0.00739 \times 2200 \approx 16.26 \text{ V} $$

6. Final Adjustments and Recalculations

Recheck if $V_1$ must be adjusted based on its position in the circuit.

Using Kirchhoff’s rearrangement:

$$ V_1 = 27 - 9 - 5 - (I \cdot 1.2) = 13.12 \text{ V} - (7.39 \text{ mA})(1.2 kΩ) $$

Plugging in to determine $V_1$, recalculate based on total contributions.

7. Choose the Closest Value from Options Provided

Check results against available answer choices (7.98 V, 7.22 V, 7.05 V, and 7.56 V).