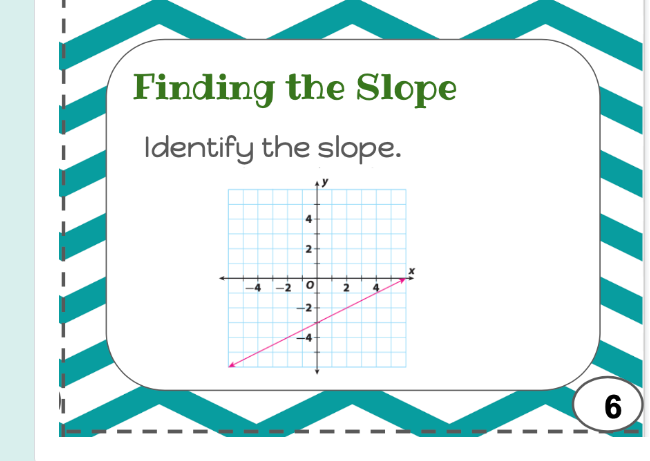
Identify the slope.
Understand the Problem
The question is asking to determine the slope of a line represented on a graph. We will calculate the slope using the change in y over the change in x between two points on the line.
Answer
The slope of the line is $1$.
Answer for screen readers
The slope of the line is $1$.
Steps to Solve
- Identify Two Points on the Line
To find the slope of the line, first, identify two points that the line passes through. From the graph, we can see the points (2, 2) and (4, 4).
- Use the Slope Formula
The slope ($m$) is calculated using the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Where:
- $(x_1, y_1) = (2, 2)$
- $(x_2, y_2) = (4, 4)$
- Plug in the Values
Substituting the coordinates into the slope formula:
$$ m = \frac{4 - 2}{4 - 2} $$
- Calculate the Slope
Now perform the calculations:
$$ m = \frac{2}{2} = 1 $$
The slope of the line is $1$.
More Information
The slope of a line indicates its steepness and direction. A slope of $1$ means that for every unit increase in $x$, $y$ also increases by the same amount. This results in a line that rises at a 45-degree angle.
Tips
- Incorrect Point Selection: Selecting points that do not lie on the line. Always ensure that the points are clearly on the line.
- Incorrect Formula Use: Confusing the slope formula with other formulas. Remember that slope specifically relates to the change in $y$ over the change in $x$.
AI-generated content may contain errors. Please verify critical information