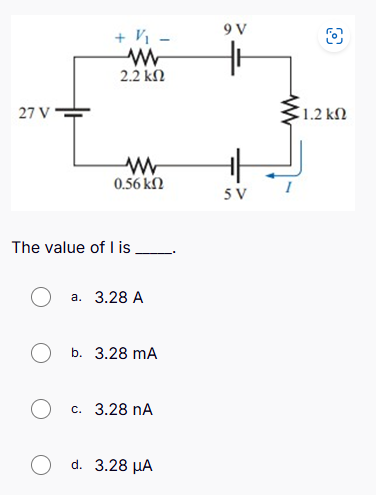
The value of I is ____.

Steps to Solve

1. Identify the circuit components

The circuit has two voltage sources (27 V, 9 V, and 5 V), and three resistors (2.2 kΩ, 0.56 kΩ, and 1.2 kΩ). We'll use Kirchhoff's voltage law (KVL) to analyze it.

2. Apply Kirchhoff’s voltage law

According to KVL, the sum of the voltage drops in the circuit should equal the sum of the voltage sources. Starting from the 27 V source and moving around the loop, we can set up the equation:

$$ 27 \text{ V} - I \cdot 2.2 \text{ k}\Omega - I \cdot 1.2 \text{ k}\Omega - 9 \text{ V} - 5 \text{ V} = 0 $$

3. Combine resistances

Before solving, combine the resistances in series as follows:

$$ (R_1 + R_2) = (2.2 \text{ k}\Omega + 1.2 \text{ k}\Omega) = 3.4 \text{ k}\Omega $$

This gives us:

$$ 27 \text{ V} - I \cdot 3.4 \text{ k}\Omega - 14 \text{ V} = 0 $$

4. Rearrange the equation

Rearranging this gives:

$$ I \cdot 3.4 \text{ k}\Omega = 27 \text{ V} - 14 \text{ V} $$ $$ I \cdot 3.4 \text{ k}\Omega = 13 \text{ V} $$

5. Solve for I

Now, isolate the current $I$:

$$ I = \frac{13 \text{ V}}{3.4 \text{ k}\Omega} $$

Convert 3.4 kΩ to ohms:

$$ 3.4 \text{ k}\Omega = 3400 \text{ Ω} $$

So we get:

$$ I = \frac{13}{3400} $$ $$ I \approx 0.00382 \text{ A} = 3.82 \text{ mA} $$

6. Convert the answer to the appropriate unit

Converting to milliamps gives:

Thus,

$$ I \approx 3.82 \text{ mA} $$