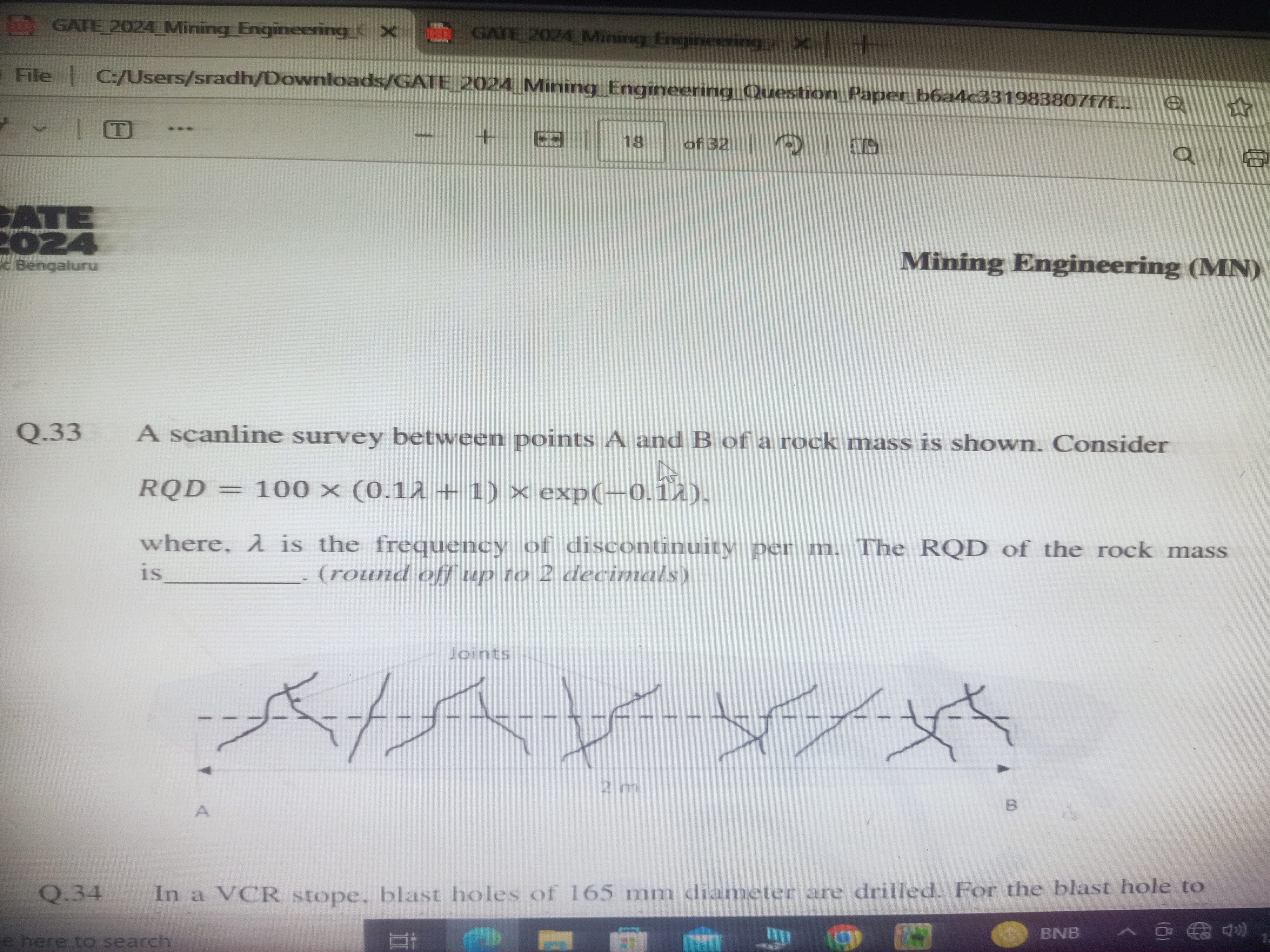
A scanline survey between points A and B of a rock mass is shown. Consider RQD = 100 × (0.1λ + 1) × exp(-0.1λ), where λ is the frequency of discontinuity per m. The RQD of the rock... A scanline survey between points A and B of a rock mass is shown. Consider RQD = 100 × (0.1λ + 1) × exp(-0.1λ), where λ is the frequency of discontinuity per m. The RQD of the rock mass is __________. (round off up to 2 decimals) Read more

Steps to Solve

1. Identify the given parameters

The equation for RQD is given as: $$ RQD = 100 \times (0.1\lambda + 1) \times e^{-0.1\lambda} $$

Where:

• $\lambda = 0.12$ (frequency of discontinuity per meter)

2. Substitute the value of λ into the equation

To find RQD, substitute $\lambda = 0.12$: $$ RQD = 100 \times (0.1 \times 0.12 + 1) \times e^{-0.1 \times 0.12} $$

3. Calculate the components of the equation

Calculate $0.1 \times 0.12 + 1$: $$ 0.1 \times 0.12 = 0.012 \quad \Rightarrow \quad 0.012 + 1 = 1.012 $$

Calculate $e^{-0.1 \times 0.12}$: $$ -0.1 \times 0.12 = -0.012 $$ Using the approximate value $e^{-0.012} \approx 0.9881$.

4. Combine the calculated values

Now substitute these values back into the equation: $$ RQD = 100 \times 1.012 \times 0.9881 $$

5. Perform the final calculation

Calculate the final value: $$ RQD = 100 \times 1.012 \times 0.9881 \approx 99.8692 $$

6. Round to two decimal places

Finally, round the answer to two decimal places: $$ RQD \approx 99.87 $$