The triangle U'V'W' is a dilation of the triangle UVW. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction, or a... The triangle U'V'W' is a dilation of the triangle UVW. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction, or a whole number.
Understand the Problem
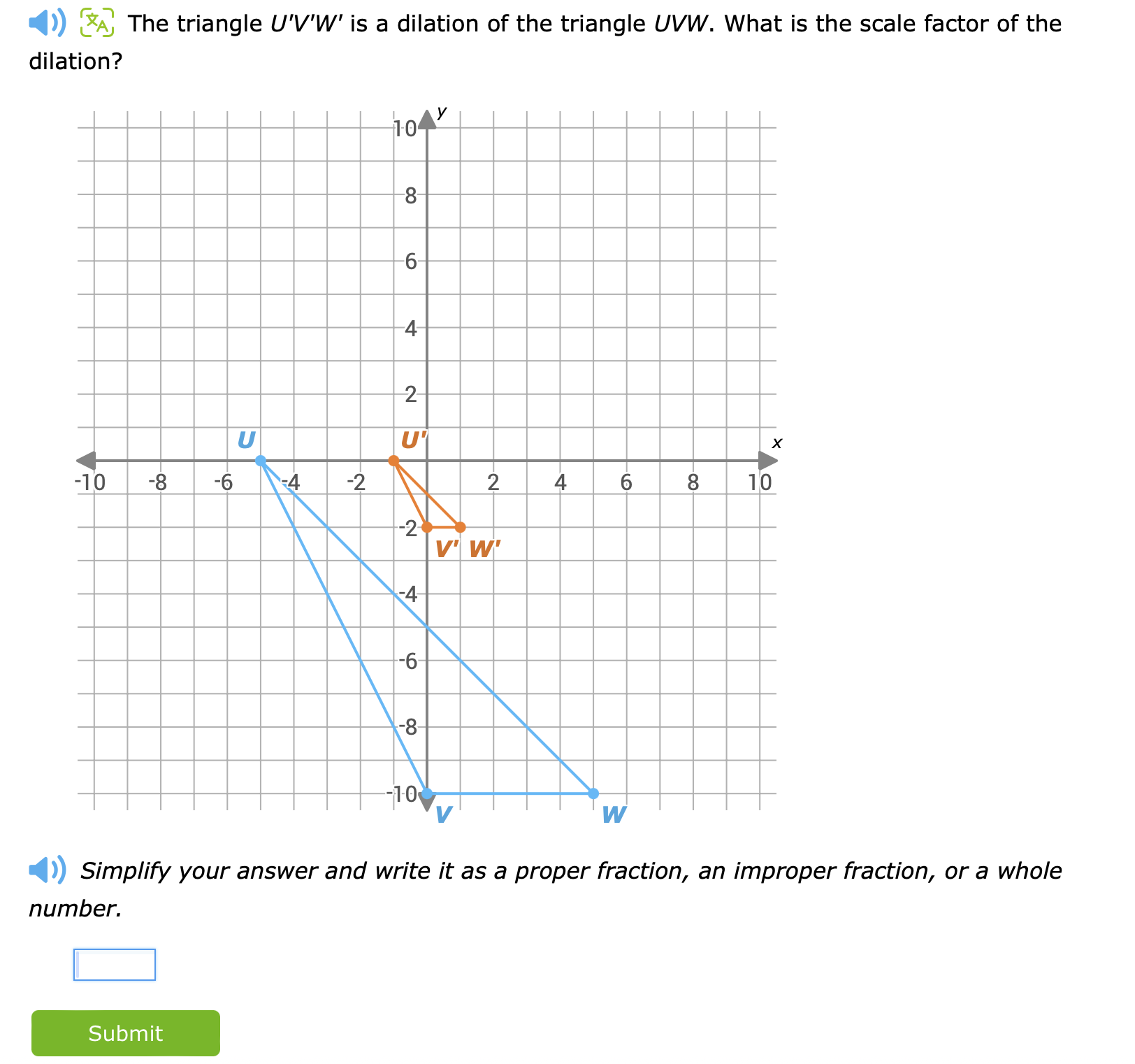
The question is asking for the scale factor of the dilation from triangle UVW to triangle U'V'W'. To find this, we will compare the lengths of the sides of the two triangles based on their coordinates provided in the graph.
Answer
The scale factor of the dilation is \( \frac{\sqrt{74}}{37} \).
Answer for screen readers
The scale factor of the dilation is ( \frac{\sqrt{74}}{37} ).
Steps to Solve
-
Identify coordinates of points U, V, W and U', V', W'
From the graph, the coordinates are:
- ( U(-6, 2) )
- ( V(-4, -10) )
- ( W(-2, -10) )
For the dilated triangle:
- ( U'(-4, -2) )
- ( V'(-2, -4) )
- ( W'(2, -4) )
-
Calculate the side lengths of triangle UVW
To find the lengths of sides UV, VW, and UW, we use the distance formula:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
-
For ( UV ): $$ UV = \sqrt{((-4) - (-6))^2 + ((-10) - 2)^2} = \sqrt{(2)^2 + (-12)^2} = \sqrt{4 + 144} = \sqrt{148} = 2\sqrt{37} $$
-
For ( VW ): $$ VW = \sqrt{((-2) - (-4))^2 + ((-10) - (-10))^2} = \sqrt{(2)^2 + (0)^2} = 2 $$
-
For ( UW ): $$ UW = \sqrt{((-2) - (-6))^2 + ((-10) - 2)^2} = \sqrt{(4)^2 + (-12)^2} = \sqrt{16 + 144} = \sqrt{160} = 4\sqrt{10} $$
-
-
Calculate the side lengths of triangle U'V'W'
Using the same formula for the corresponding sides of triangle U'V'W':
-
For ( U'V' ): $$ U'V' = \sqrt{((-2) - (-4))^2 + ((-4) - (-2))^2} = \sqrt{(2)^2 + (-2)^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2} $$
-
For ( V'W' ): $$ V'W' = \sqrt{(2 - (-2))^2 + ((-4) - (-4))^2} = \sqrt{(4)^2 + (0)^2} = 4 $$
-
For ( U'W' ): $$ U'W' = \sqrt{(2 - (-4))^2 + ((-4) - (-2))^2} = \sqrt{(6)^2 + (-2)^2} = \sqrt{36 + 4} = \sqrt{40} = 2\sqrt{10} $$
-
-
Find the scale factor of dilation
Compare the corresponding sides to find the scale factor ( k ):
$$ k = \frac{U'V'}{UV} $$
Using side ( UV ) and ( U'V' ):
$$ k = \frac{2\sqrt{2}}{2\sqrt{37}} \Rightarrow k = \frac{\sqrt{2}}{\sqrt{37}} \Rightarrow k = \frac{\sqrt{74}}{37} $$
The scale factor of the dilation is ( \frac{\sqrt{74}}{37} ).
More Information
Dilation is a transformation that changes the size of a figure while maintaining its shape. The scale factor determines how much larger or smaller the dilated figure is compared to the original.
Tips
- Failing to correctly identify the corresponding sides between the original and dilated triangles.
- Not simplifying the final ratio or failing to express it in simplest form.
AI-generated content may contain errors. Please verify critical information