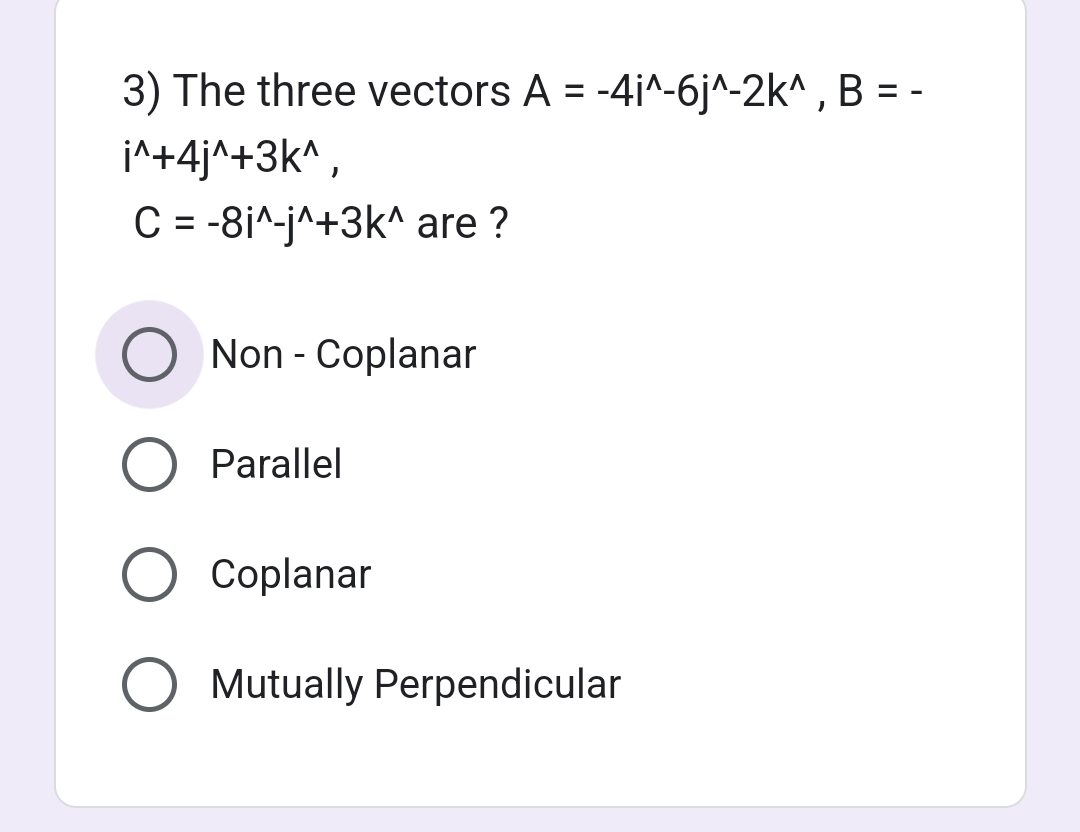
The three vectors A = -4i - 6j - 2k, B = -i + 4j + 3k, C = -8i - j + 3k are?

Steps to Solve

1. Construct the vectors Identify the vectors given in the problem:
   $$ \mathbf{A} = -4 \mathbf{i} - 6 \mathbf{j} - 2 \mathbf{k} $$
   $$ \mathbf{B} = -\mathbf{i} + 4 \mathbf{j} + 3 \mathbf{k} $$
   $$ \mathbf{C} = -8 \mathbf{i} - \mathbf{j} + 3 \mathbf{k} $$

2. Set up the determinant To check if the vectors are coplanar, we can use the determinant of the matrix formed by the vectors. The vectors are coplanar if the determinant is zero.

Set up the matrix with the vectors as rows: $$ \begin{vmatrix} -4 & -6 & -2 \ -1 & 4 & 3 \ -8 & -1 & 3 \end{vmatrix} $$

3. Calculate the determinant Calculating the determinant using the formula for a 3x3 matrix: $$ \text{Det} = a(ei - fh) - b(di - fg) + c(dh - eg) $$
   For our matrix:

• ( a = -4, b = -6, c = -2 )
• ( d = -1, e = 4, f = 3 )
• ( g = -8, h = -1, i = 3 )

This gives: $$ \text{Det} = -4(4 \cdot 3 - 3 \cdot -1) - (-6)(-1 \cdot 3 - 3 \cdot -8) + (-2)(-1 \cdot -1 - 4 \cdot -8) $$

4. Simplify and solve for the determinant Calculate the individual components:

• First term: ( -4(12 + 3) = -4 \cdot 15 = -60 )
• Second term: ( -6(-3 + 24) = -6 \cdot 21 = -126 )
• Third term: ( -2(1 + 32) = -2 \cdot 33 = -66 )

Putting it together: $$ \text{Det} = -60 + 126 - 66 = 0 $$

5. Conclusion Since the determinant is 0, the vectors are coplanar.