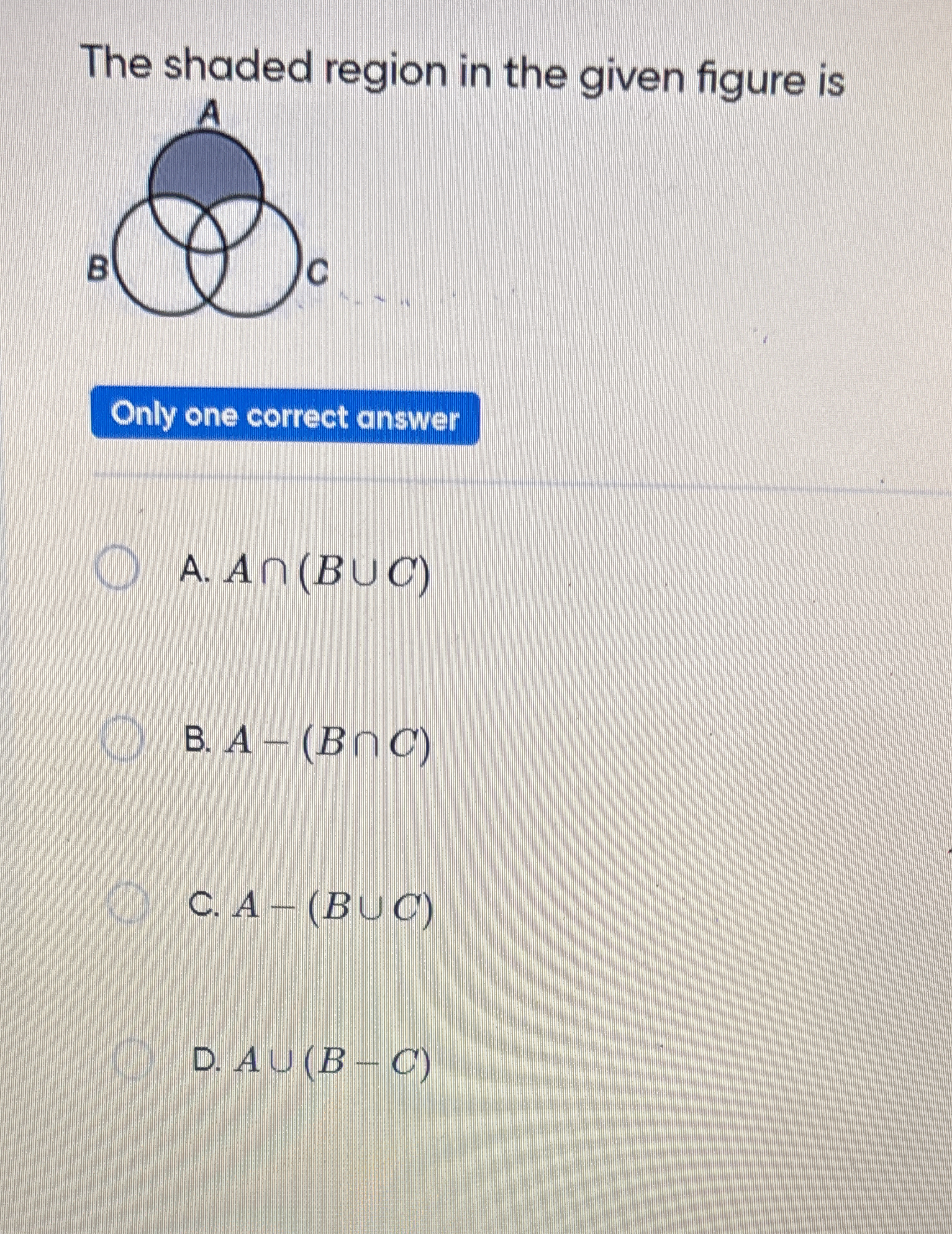
The shaded region in the given figure is

Steps to Solve

1. Identify the Shaded Area Examine the Venn diagram to determine what regions are shaded. In this case, the shaded region represents elements that are in set A and not in any overlapping areas with sets B or C.

2. Express the Shaded Area using Set Notation We need to express the shaded area mathematically. The shaded region includes elements that are only in set A and excludes elements that overlap with sets B and C. Thus, the expression would be ( A \cap (B^c \cap C^c) ), where ( B^c ) and ( C^c ) represent the complements of sets B and C respectively.

3. Match the Expression with Given Options Review the provided options to find one that corresponds to the expression derived for the shaded area.

4. Analyze the Options Based on the description:

   • Option A: ( A \cap (B \cup C) ) - This includes elements in A that overlap with B or C.
   • Option B: ( A - (B \cap C) ) - This suggests A excluding the intersection of B and C.
   • Option C: ( A - (B \cup C) ) - This corresponds to A excluding any elements in B or C.
   • Option D: ( A \cup (B - C) ) - This includes all of A and elements in B that are not in C.

5. Correct Identification The correct option is option C, as it accurately captures the elements in A that are not in B or C.