If f(x) = x/(x^2 - 4) for -2 < x < 2, find f^(-1)(1/2).
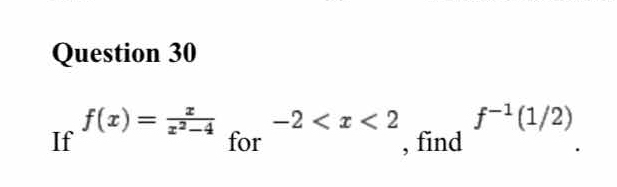
Understand the Problem
The question is asking us to find the inverse of the function f(x) at a specific value (1/2), given the function definition and its domain. To solve this, we will first express f(x) as given, then set up the equation to find the inverse function and solve for the appropriate value.
Answer
$$ f^{-1}(1/2) = 1 - \sqrt{5} $$
Answer for screen readers
The final answer is:
$$ f^{-1}(1/2) = 1 - \sqrt{5} $$
Steps to Solve
- Set up the equation for the inverse function
To find ( f^{-1}(1/2) ), we need to find when ( f(x) = \frac{1}{2} ). Thus, we set the equation:
$$ \frac{x}{x^2 - 4} = \frac{1}{2} $$
- Cross multiply to eliminate the fraction
Cross-multiply to simplify the equation:
$$ 2x = x^2 - 4 $$
- Rearrange the equation
Rearrange the equation to set it to zero:
$$ x^2 - 2x - 4 = 0 $$
- Use the quadratic formula
We can solve for ( x ) using the quadratic formula ( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ). Here, ( a = 1 ), ( b = -2 ), and ( c = -4 ).
Calculate the discriminant:
$$ b^2 - 4ac = (-2)^2 - 4 \times 1 \times (-4) = 4 + 16 = 20 $$
Now apply the quadratic formula:
$$ x = \frac{-(-2) \pm \sqrt{20}}{2 \times 1} = \frac{2 \pm \sqrt{20}}{2} = 1 \pm \sqrt{5} $$
- Evaluate possible solutions
This gives us two possible values:
$$ x_1 = 1 + \sqrt{5}, \quad x_2 = 1 - \sqrt{5} $$
- Determine valid solutions within the domain
Check which of these values lies within the domain ( -2 < x < 2 ):
- For ( x_1 = 1 + \sqrt{5} \approx 3.24 ) (not valid)
- For ( x_2 = 1 - \sqrt{5} \approx -1.24 ) (valid)
Thus, ( f^{-1}(1/2) = 1 - \sqrt{5} ).
The final answer is:
$$ f^{-1}(1/2) = 1 - \sqrt{5} $$
More Information
The inverse function provides a way to find the original input for a given output. In this case, ( f^{-1}(1/2) ) tells us which value of ( x ) produces an output of ( \frac{1}{2} ) for the function ( f(x) ).
Tips
- Misapplying the quadratic formula or making arithmetic errors while calculating the discriminant.
- Not verifying if the solutions fall within the defined domain of the function.
AI-generated content may contain errors. Please verify critical information