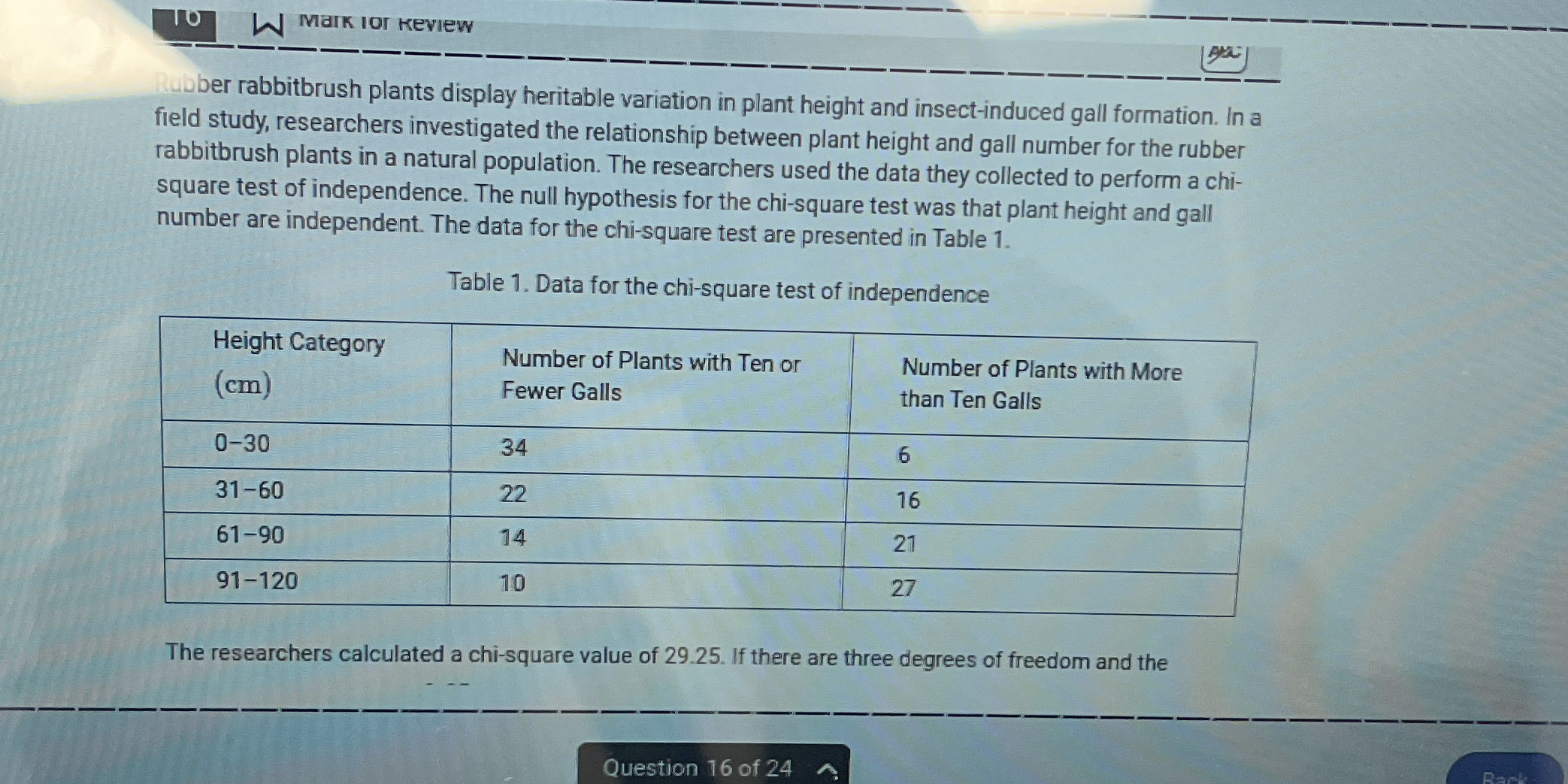
The researchers calculated a chi-square value of 29.25. If there are three degrees of freedom, what does this mean?

Steps to Solve

1. Understanding the Chi-Square Test The chi-square test of independence checks whether two categorical variables are independent. Here, the variables are plant height and gall number.

2. Set up the Contingency Table Based on the data provided in Table 1, we can summarize it in a contingency table:

   Height Category (cm)	≤ 10 Galls	> 10 Galls	Total
   0-30	34	6	40
   31-60	22	16	38
   61-90	14	21	35
   91-120	10	27	37
   Total	80	70	150

3. Calculate Expected Frequencies For each cell, the expected frequency is calculated as: $$ E = \frac{(\text{Row Total}) \times (\text{Column Total})}{\text{Grand Total}} $$ For example, for the height category 0-30, galls ≤ 10: $$ E_{0-30, \leq 10} = \frac{40 \times 80}{150} = 21.33 $$

4. Compute the Chi-Square Statistic The chi-square statistic is calculated using: $$ \chi^2 = \sum \frac{(O - E)^2}{E} $$ where ( O ) is the observed frequency and ( E ) is the expected frequency.

5. Degrees of Freedom The degrees of freedom for a chi-square test of independence is given by: $$ df = (r - 1) \times (c - 1) $$ where ( r ) is the number of rows and ( c ) is the number of columns. Here, ( df = (4 - 1)(2 - 1) = 3 ).

6. Interpret the Chi-Square Value A calculated chi-square value of 29.25 with 3 degrees of freedom can be compared to a critical value from the chi-square distribution table for a chosen significance level (e.g., 0.05).

7. Decision on the Null Hypothesis If the calculated chi-square is greater than the critical value, we reject the null hypothesis, indicating that plant height and gall number are dependent.