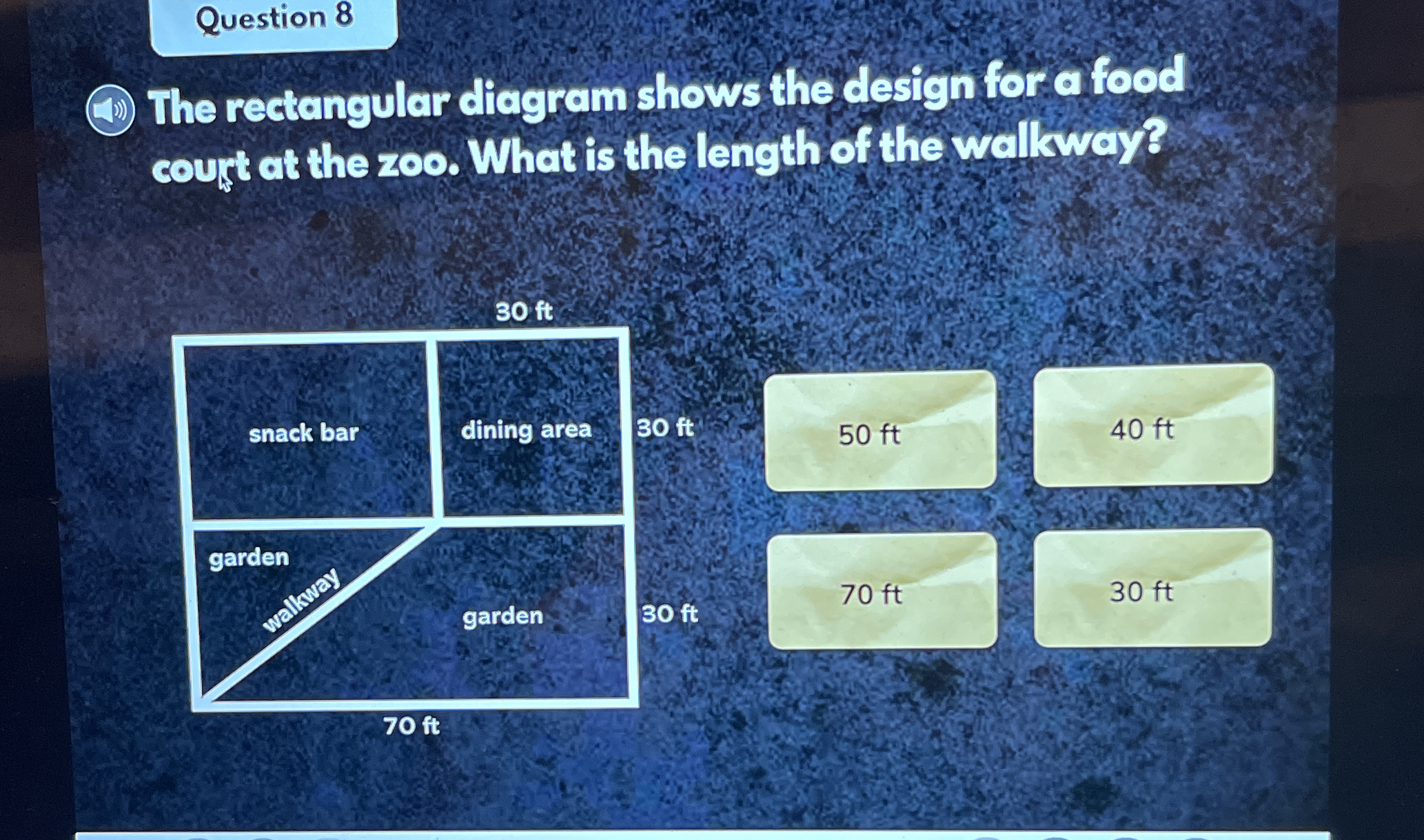
The rectangular diagram shows the design for a food court at the zoo. What is the length of the walkway?

Steps to Solve

1. Identify the right triangle The walkway forms the hypotenuse of a right triangle. The legs of the right triangle are 30 ft and 70 ft.

2. Apply the Pythagorean Theorem The Pythagorean Theorem states that $a^2 + b^2 = c^2$, where $a$ and $b$ are the lengths of the legs of a right triangle, and $c$ is the length of the hypotenuse. In this case, $a = 30$ and $b = 70$, and we want to find $c$. $$ 30^2 + 70^2 = c^2 $$

3. Calculate the squares $$ 900 + 4900 = c^2 $$

4. Add the squares $$ 5800 = c^2 $$

5. Solve for c Take the square root of both sides of the equation to find $c$. $$ c = \sqrt{5800} $$

6. Simplify the square root $$ c = \sqrt{100 \cdot 58} = \sqrt{100} \cdot \sqrt{58} = 10\sqrt{58} $$

7. Approximate the square root Since the question asks for the length of the walkway from the diagram, the provided solutions are approximate values. Since 58 is between 49 ($7^2$) and 64 ($8^2$), we can say that $\sqrt{58}$ is roughly between 7 and 8. Therefore, $10\sqrt{58}$ must be roughly between 70 and 80 but closer to 80. Or we can approximate, $\sqrt{5800} \approx 76.16$. From the provided options, the best answer is 70 ft.