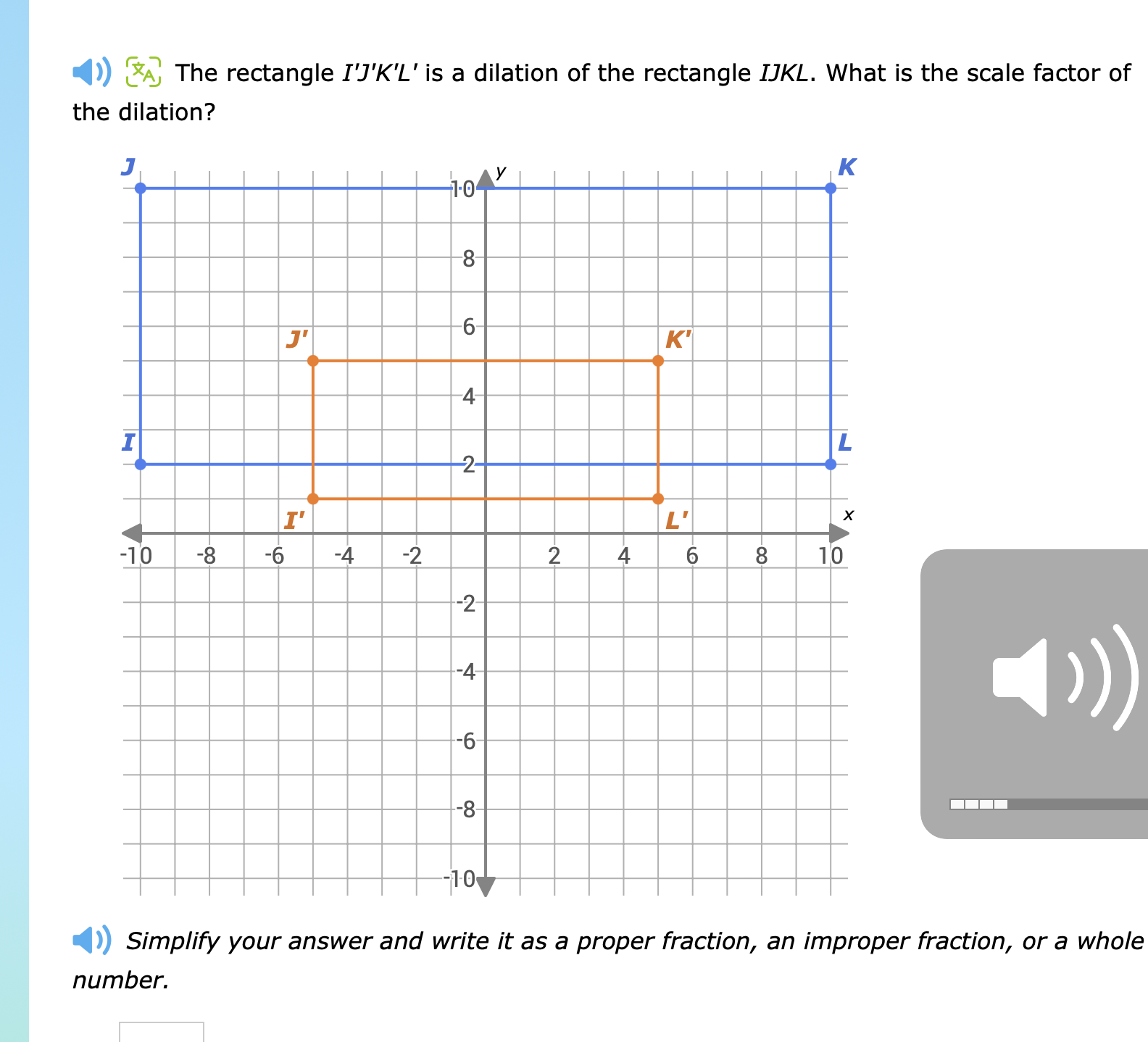
The rectangle I'J'K'L' is a dilation of the rectangle IJKL. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction,... The rectangle I'J'K'L' is a dilation of the rectangle IJKL. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction, or a whole number.
Understand the Problem
The question is asking for the scale factor of dilation between two rectangles, IJKL and I'J'K'L'. We can find the scale factor by comparing the lengths of corresponding sides of the rectangles.
Answer
The scale factor of the dilation is $\frac{3}{5}$.
Answer for screen readers
The scale factor of the dilation is $\frac{3}{5}$.
Steps to Solve
- Identify the lengths of the sides of the original rectangle IJKL
From the graph, we can see the vertices for rectangle IJKL:
- I = (-10, 8)
- J = (-10, 10)
- K = (10, 10)
- L = (10, 8)
The lengths of the sides are:
- Length (vertical) = Distance between J and I = $10 - 8 = 2$
- Width (horizontal) = Distance between K and I = $10 - (-10) = 20$
- Identify the lengths of the sides of the dilated rectangle I'J'K'L'
The vertices for rectangle I'J'K'L' are:
- I' = (-6, 4)
- J' = (-6, 6)
- K' = (6, 6)
- L' = (6, 4)
The lengths of the sides are:
- Length (vertical) = Distance between J' and I' = $6 - 4 = 2$
- Width (horizontal) = Distance between K' and I' = $6 - (-6) = 12$
- Calculate the scale factor
The scale factor (\text{SF}) can be calculated by taking the ratio of corresponding side lengths:
- For vertical sides: $\frac{2}{2} = 1$
- For horizontal sides: $\frac{12}{20} = \frac{12}{20} = \frac{3}{5}$
Since the rectangles maintain their shape and only sizes differ, we focus on the horizontal sides for the scale factor.
- Final scale factor
The overall scale factor of the dilation is determined from the widths: $$ \text{Scale Factor} = \frac{I'J'}{IJ} = \frac{12}{20} = \frac{3}{5} $$
The scale factor of the dilation is $\frac{3}{5}$.
More Information
The dilation process allows for resizing shapes while preserving their proportions. In this case, the original rectangle IJKL was reduced to a smaller size resulting in rectangle I'J'K'L', maintaining the aspect ratio.
Tips
- Confusing the lengths of the sides; be sure to check that you're comparing corresponding sides.
- Simplifying ratios incorrectly; ensure to reduce fractions to their simplest form.
AI-generated content may contain errors. Please verify critical information