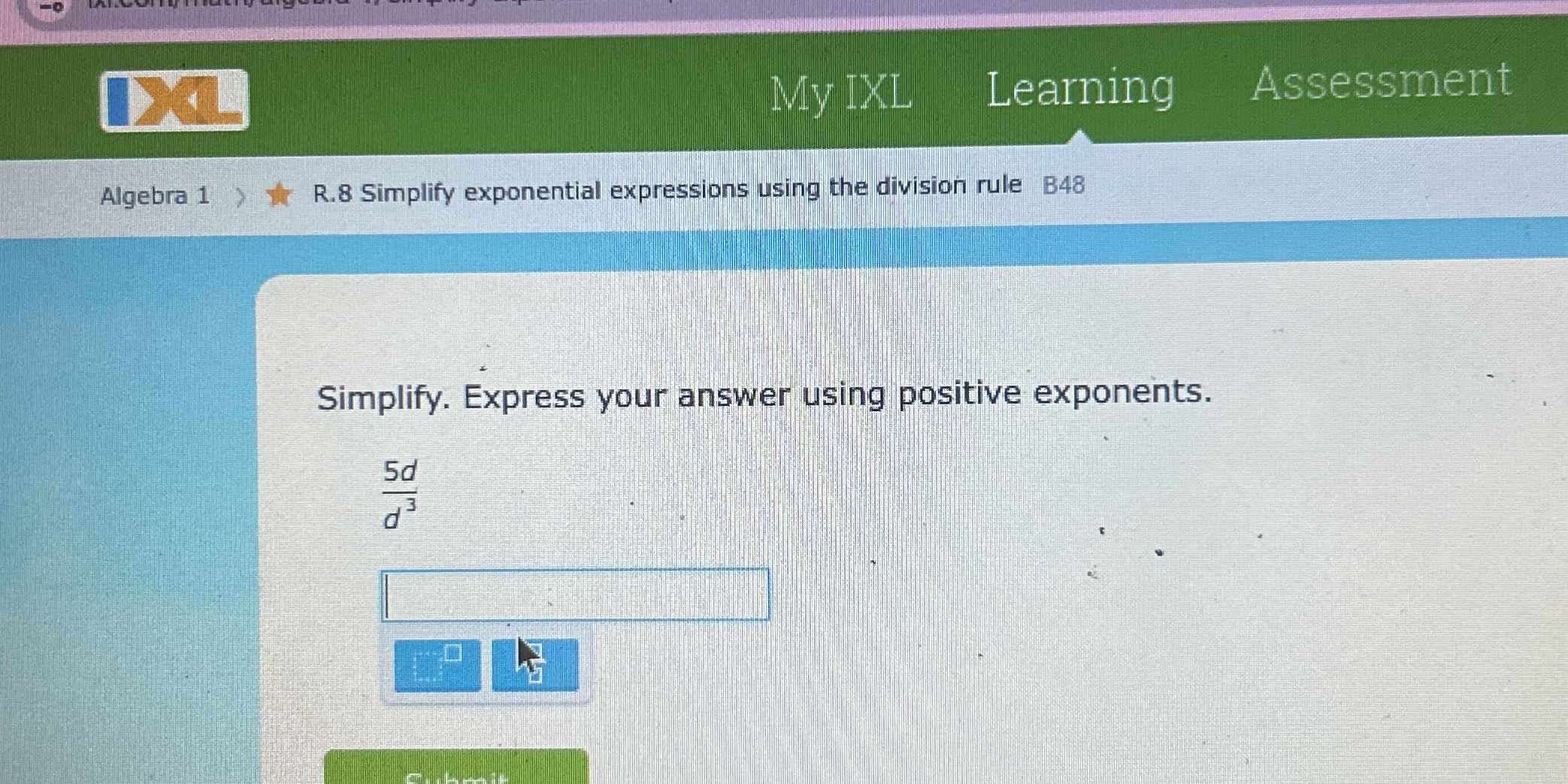
Simplify. Express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression \frac{5d}{d^3} using the division rule for exponents, ensuring that the answer is expressed with positive exponents.
Answer
The simplified expression is $$ \frac{5}{d^2} $$
Answer for screen readers
The simplified expression is
$$ \frac{5}{d^2} $$
Steps to Solve
- Write the expression clearly We start with the expression
$$ \frac{5d}{d^3} $$
- Apply the division rule for exponents According to the division rule of exponents, when dividing like bases, we subtract the exponents. The base here is ( d ), which has an exponent of 1 in the numerator. Therefore, we have:
$$ d^{1-3} = d^{-2} $$
- Combine the expression Now, substitute back into the expression:
$$ \frac{5d}{d^3} = 5 \cdot d^{-2} $$
- Convert to positive exponents To express the answer with a positive exponent, we rewrite ( d^{-2} ) as:
$$ \frac{5}{d^2} $$
The simplified expression is
$$ \frac{5}{d^2} $$
More Information
When simplifying expressions with exponents, the division rule (subtracting exponents) is key. Remember that any negative exponent can be converted to a positive exponent by moving the base to the denominator.
Tips
- Not applying the division rule correctly by failing to subtract exponents properly.
- Leaving the answer with negative exponents instead of converting them to positive.
AI-generated content may contain errors. Please verify critical information