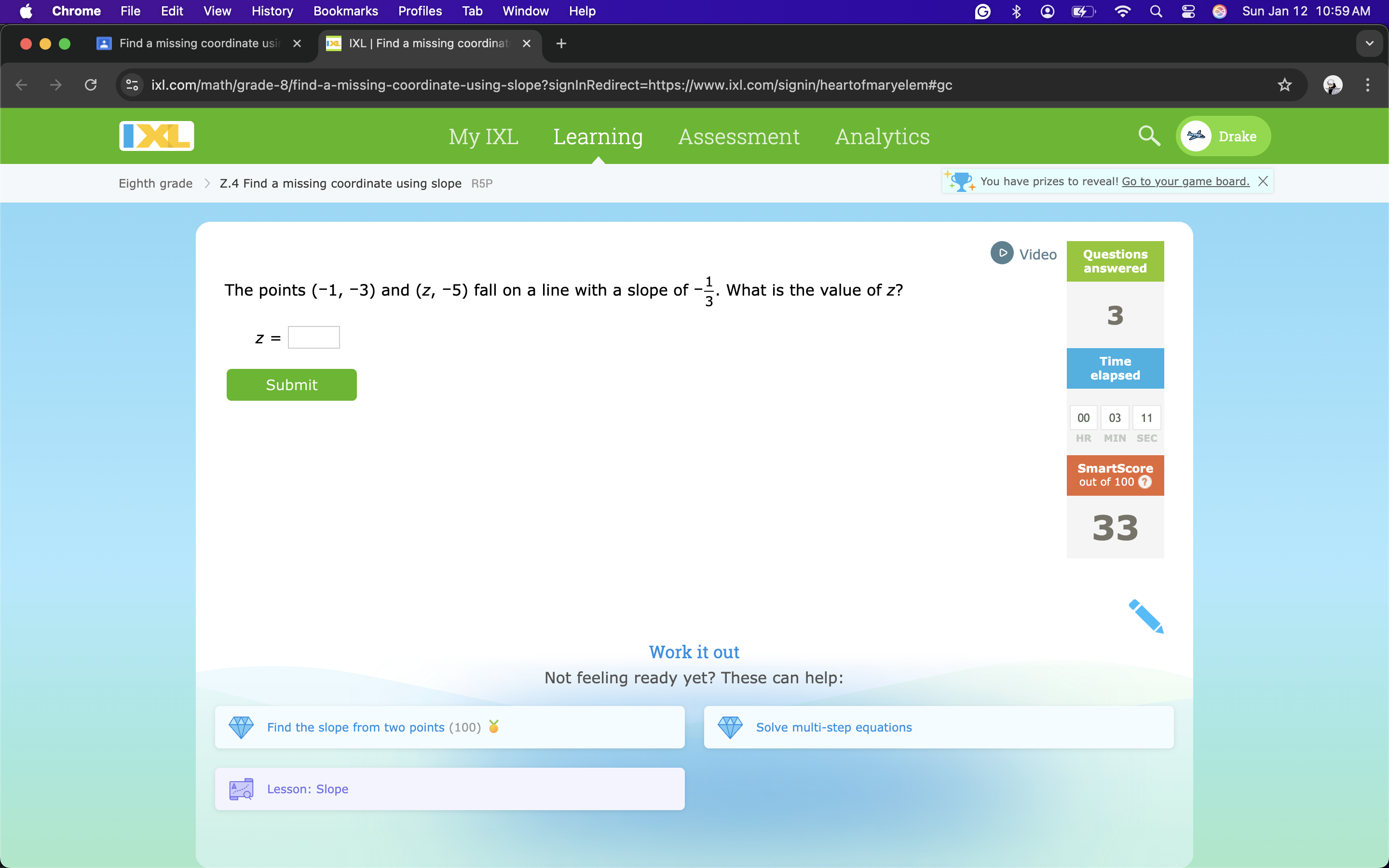
The points (-1, -3) and (z, -5) fall on a line with a slope of -1/3. What is the value of z?
Understand the Problem
The question is asking for the value of z given two points and the slope of a line connecting them. We will need to use the slope formula to solve for z.
Answer
$z = 5$
Answer for screen readers
The value of (z) is (5).
Steps to Solve
-
Identify the points and slope The two points given are ((-1, -3)) and ((z, -5)). The slope of the line connecting these points is given as $-\frac{1}{3}$.
-
Use the slope formula The slope formula is given by: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$ In our case:
- (y_1 = -3)
- (y_2 = -5)
- (x_1 = -1)
- (x_2 = z) Substituting the values into the slope formula gives: $$ -\frac{1}{3} = \frac{-5 - (-3)}{z - (-1)} $$
-
Simplify the right side Calculate the difference in the numerator: $$ -\frac{1}{3} = \frac{-5 + 3}{z + 1} $$ This simplifies to: $$ -\frac{1}{3} = \frac{-2}{z + 1} $$
-
Cross-multiply to solve for (z) Cross-multiplying gives: $$ -1(z + 1) = -6 $$ This simplifies to: $$ -z - 1 = -6 $$
-
Isolate (z) Add (1) to both sides: $$ -z = -5 $$ Multiply by (-1): $$ z = 5 $$
The value of (z) is (5).
More Information
The slope of a line measures its steepness and direction, often calculated using two points. It is important to set up the slope formula correctly to find missing coordinates.
Tips
- Forgetting to convert negative signs properly: Be careful with signs when substituting and simplifying equations.
- Misinterpreting the slope formula: Ensure that you assign (x_1), (y_1), (x_2), and (y_2) correctly from the points.
AI-generated content may contain errors. Please verify critical information