How to calculate the resultant vector from 10 km/hr and 2 km/hr and determine its direction?
Understand the Problem
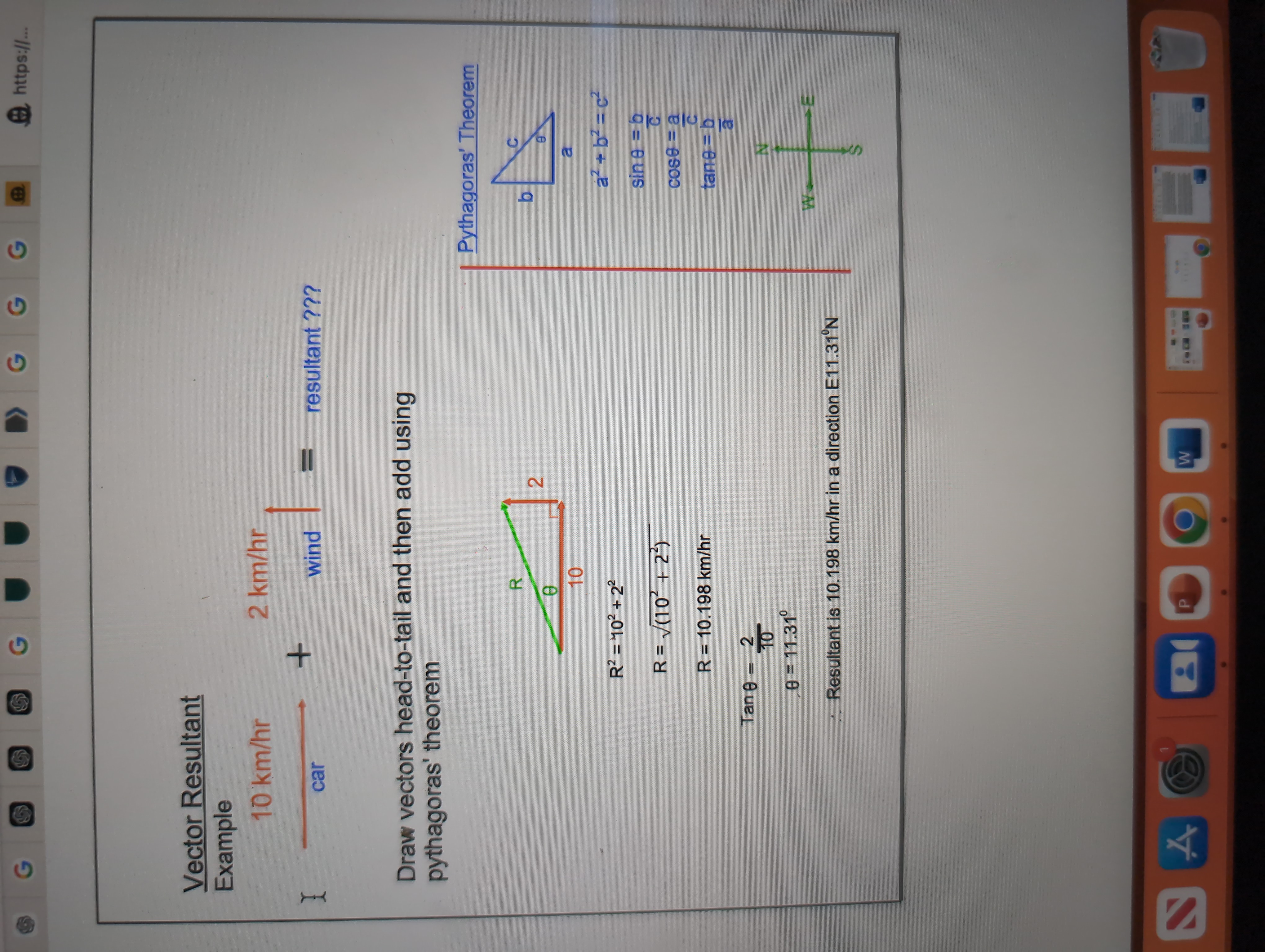
The question is asking to calculate the resultant vector from two velocities using vector addition, particularly focusing on head-to-tail placement and applying Pythagorean theorem principles.
Answer
The resultant vector is approximately $10.198 \text{ km/hr}$ in the direction $E11.31^\circ N$.
Answer for screen readers
The resultant vector is approximately $10.198 \text{ km/hr}$ in the direction $E11.31^\circ N$.
Steps to Solve
-
Identify the vectors We have two vectors: one with a magnitude of $10 \text{ km/hr}$ (car) and the other with $2 \text{ km/hr}$ (wind). We will represent the car's velocity horizontally and the wind's velocity vertically.
-
Draw the vectors head-to-tail Position the car's vector horizontally to the right and the wind's vector vertically upwards, forming a right triangle with these two vectors.
-
Apply the Pythagorean theorem To find the magnitude of the resultant vector $R$, use the Pythagorean theorem: $$ R = \sqrt{(10^2) + (2^2)} $$
-
Calculate the magnitude Substituting the values into the equation: $$ R = \sqrt{(10^2) + (2^2)} = \sqrt{100 + 4} = \sqrt{104} $$ Calculating $\sqrt{104}$ gives approximately: $$ R \approx 10.198 \text{ km/hr} $$
-
Determine the direction To find the angle $\theta$, use the tangent function: $$ \tan \theta = \frac{2}{10} $$ Then, solve for $\theta$: $$ \theta = \tan^{-1}\left(\frac{2}{10}\right) $$ Calculating this yields: $$ \theta \approx 11.31^\circ $$
-
State the final resultant vector The resultant vector is: $$ R \approx 10.198 \text{ km/hr}, \text{ Direction: } E11.31^\circ N $$
The resultant vector is approximately $10.198 \text{ km/hr}$ in the direction $E11.31^\circ N$.
More Information
The calculation involves vector addition by using the Pythagorean theorem for the magnitude and trigonometric functions to find the direction. This method is widely used in physics and engineering to analyze motion.
Tips
- Misplacing vectors: Ensure vectors are drawn correctly head-to-tail; otherwise, the resultant may be inaccurate.
- Incorrect use of the Pythagorean theorem: Only applicable for right triangles – verify the angle between vectors.
- Skipping angle calculation: Be sure to compute the resultant's direction after finding its magnitude.
AI-generated content may contain errors. Please verify critical information