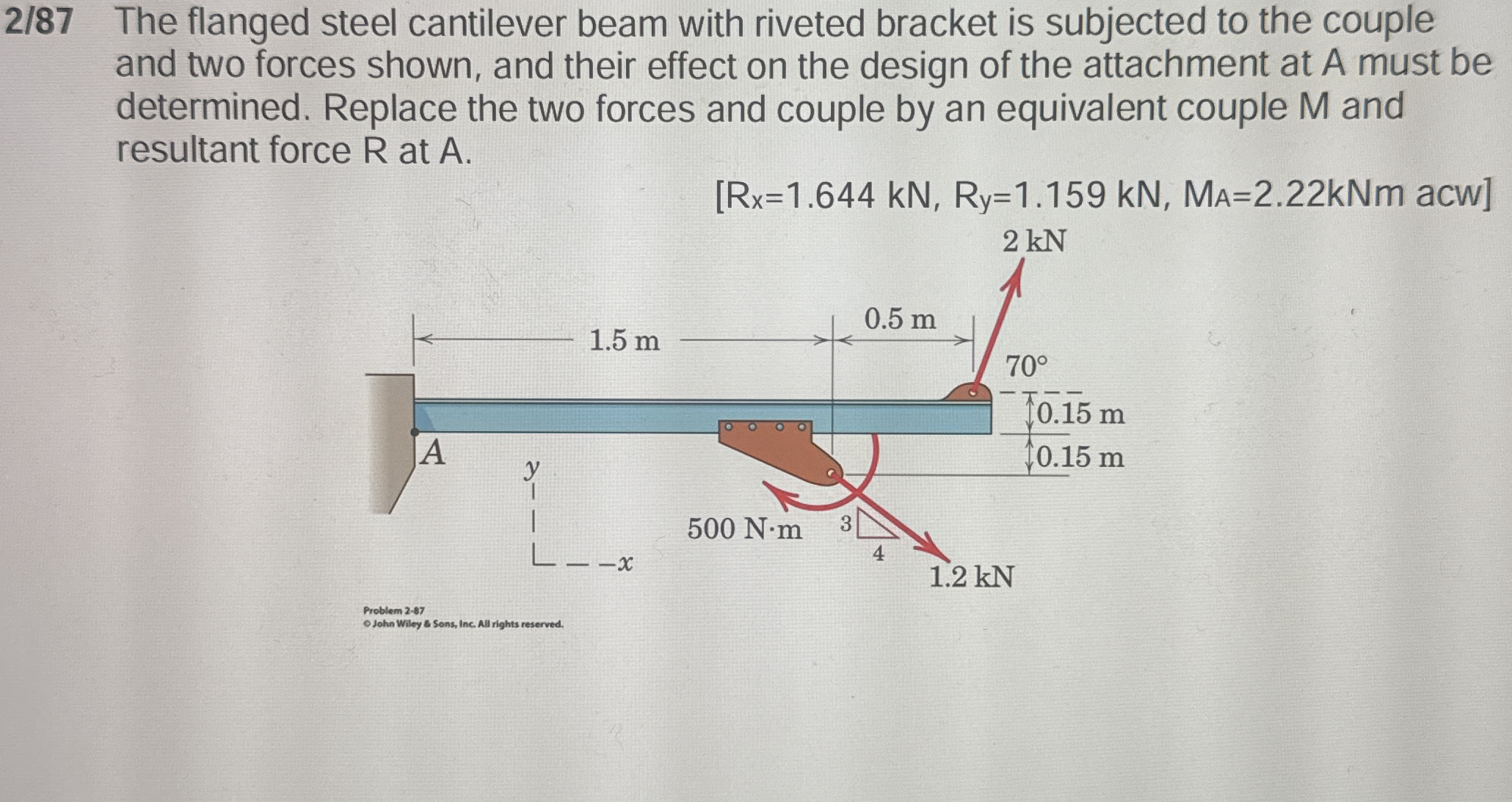
The flanged steel cantilever beam with riveted bracket is subjected to the couple and two forces shown, and their effect on the design of the attachment at A must be determined. Re... The flanged steel cantilever beam with riveted bracket is subjected to the couple and two forces shown, and their effect on the design of the attachment at A must be determined. Replace the two forces and couple by an equivalent couple M and resultant force R at A. Read more

Steps to Solve

1. Identify and Define the Forces and Moments

Identify the two forces acting on the beam and the couple moment given:

• Force 1 ($F_1 = 2 , \text{kN}$) acting at an angle of $70^\circ$ and located $0.5 , \text{m}$ from point A.
• Force 2 ($F_2 = 1.2 , \text{kN}$) acting vertically downward at a distance of $1.5 , \text{m}$ from point A.
• Couple moment ($M_A = 500 , \text{N} \cdot \text{m}$) acting at point A.

2. Resolve the Forces into Components

Resolve the first force into horizontal ($R_x$) and vertical components ($R_y$):

• $R_{1x} = F_1 \cos(70^\circ)$
• $R_{1y} = F_1 \sin(70^\circ)$

Calculate the components:

• $R_{1x} = 2 , \text{kN} \cdot \cos(70^\circ) \approx 0.684 , \text{kN}$
• $R_{1y} = 2 , \text{kN} \cdot \sin(70^\circ) \approx 1.879 , \text{kN}$

3. Calculate Resultant Force

Sum the horizontal and vertical components of the forces to find the resultant force $R$ at point A:

• $R_x = R_{1x} + 0 + 0 = 0.684 , \text{kN}$
• $R_y = R_{1y} - F_2 = 1.879 , \text{kN} - 1.2 , \text{kN} \approx 0.679 , \text{kN}$

So, the resultant force is:

$$ R = \sqrt{R_x^2 + R_y^2} $$

4. Calculate the Magnitude of Resultant Force

Using the resultant components:

• $$ R = \sqrt{(0.684 , \text{kN})^2 + (0.679 , \text{kN})^2} \approx 0.973 , \text{kN} $$

5. Determine the Equivalent Couple Moment at Point A

Now, calculate the total moment about point A due to each force:

• Moment from $F_1$: $M_{F1} = F_1 \cdot d_1 = 2 , \text{kN} \cdot 0.5 , \text{m} = 1.0 , \text{kN m}$ (clockwise)
• Moment from $F_2$: $M_{F2} = F_2 \cdot 1.5 , \text{m} = 1.2 , \text{kN} \cdot 1.5 , \text{m} = 1.8 , \text{kN m}$ (counterclockwise)

Total moment at point A:

• Resultant moment $M_A = M_{F1} - M_{F2} + M_{given} = 1.0 , \text{kN m} - 1.8 , \text{kN m} + 0.5 , \text{kN m} = -0.3 , \text{kN m}$

6. Final Resultant Couple Moment

The equivalent couple moment $M_A$:

Thus, $M_A$ is:

$$ M_A = -0.3 , \text{kN m} $$

Finally, the resultant force and couple at point A:

• Resultant force $R \approx 0.973 , \text{kN}$,
• Equivalent couple moment $M_A = -0.3 , \text{kN m}$.