The expansion of the determinant along the second row is:
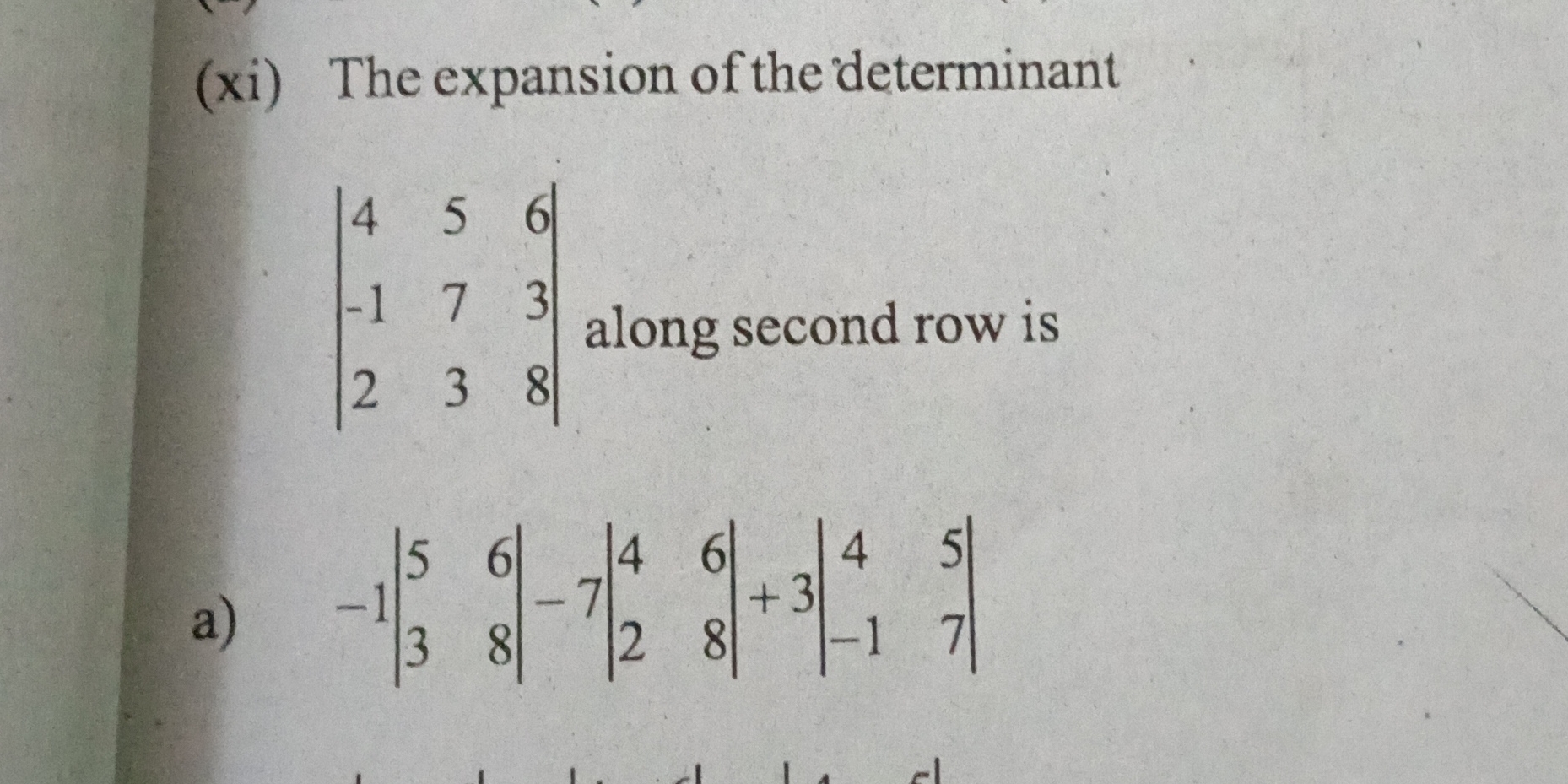
Understand the Problem
The question is asking for the expansion of a determinant along the second row. This involves applying the formula for the determinant expansion using the elements of the second row and their corresponding minors.
Answer
The expansion of the determinant along the second row is 156.
Answer for screen readers
The expansion of the determinant along the second row is 156.
Steps to Solve
- Identify the Elements of the Second Row
The second row of the matrix is:
$$ \begin{bmatrix} -1 & 7 & 3 \end{bmatrix} $$
- Write the Expansion Formula
The expansion of the determinant along the second row is given by:
$$ \text{det}(A) = a_{21}C_{21} + a_{22}C_{22} + a_{23}C_{23} $$
where ( a_{ij} ) is the element from the matrix, and ( C_{ij} ) is the corresponding cofactor, defined as:
$$ C_{ij} = (-1)^{i+j} \cdot \text{det}(M_{ij}) $$
- Calculate the Cofactors
-
For ( a_{21} = -1 ):
- Minor matrix ( M_{21} ):
$$ \begin{bmatrix} 5 & 6 \ 3 & 8 \end{bmatrix} $$
- Determinant of ( M_{21} ):
$$ \text{det}(M_{21}) = (5)(8) - (6)(3) = 40 - 18 = 22 $$
- Therefore, ( C_{21} = (-1)^{2+1} \cdot 22 = -22 ).
-
For ( a_{22} = 7 ):
- Minor matrix ( M_{22} ):
$$ \begin{bmatrix} 4 & 6 \ 2 & 8 \end{bmatrix} $$
- Determinant of ( M_{22} ):
$$ \text{det}(M_{22}) = (4)(8) - (6)(2) = 32 - 12 = 20 $$
- Therefore, ( C_{22} = (-1)^{2+2} \cdot 20 = 20 ).
-
For ( a_{23} = 3 ):
- Minor matrix ( M_{23} ):
$$ \begin{bmatrix} 4 & 5 \ 2 & 3 \end{bmatrix} $$
- Determinant of ( M_{23} ):
$$ \text{det}(M_{23}) = (4)(3) - (5)(2) = 12 - 10 = 2 $$
- Therefore, ( C_{23} = (-1)^{2+3} \cdot 2 = -2 ).
- Combine the Results
Now substitute the values into the expansion formula:
$$ \text{det}(A) = -1(-22) + 7(20) + 3(-2) $$
Calculating each term gives:
$$ \text{det}(A) = 22 + 140 - 6 $$
- Final Calculation
Combine the results to find the final determinant value:
$$ \text{det}(A) = 22 + 140 - 6 = 156 $$
The expansion of the determinant along the second row is 156.
More Information
Determinants are essential in linear algebra, often used to determine the invertibility of matrices. The method of expansion helps simplify calculations for larger determinants.
Tips
- Forgetting the sign change due to the position of the element (using ( (-1)^{i+j} )).
- Incorrectly calculating the minors or not including all necessary rows and columns in the minor matrix.
- Not summing all cofactor products correctly.
AI-generated content may contain errors. Please verify critical information