The curve with equation y = f(x) where f(x) = x^2 + ln(2x^2 - 4x + 5) has a single turning point at x = α. Show that α is a solution of the equation ax^3 + bx^2 + cx + d = 0 where... The curve with equation y = f(x) where f(x) = x^2 + ln(2x^2 - 4x + 5) has a single turning point at x = α. Show that α is a solution of the equation ax^3 + bx^2 + cx + d = 0 where a, b, c and d are integers to be found.
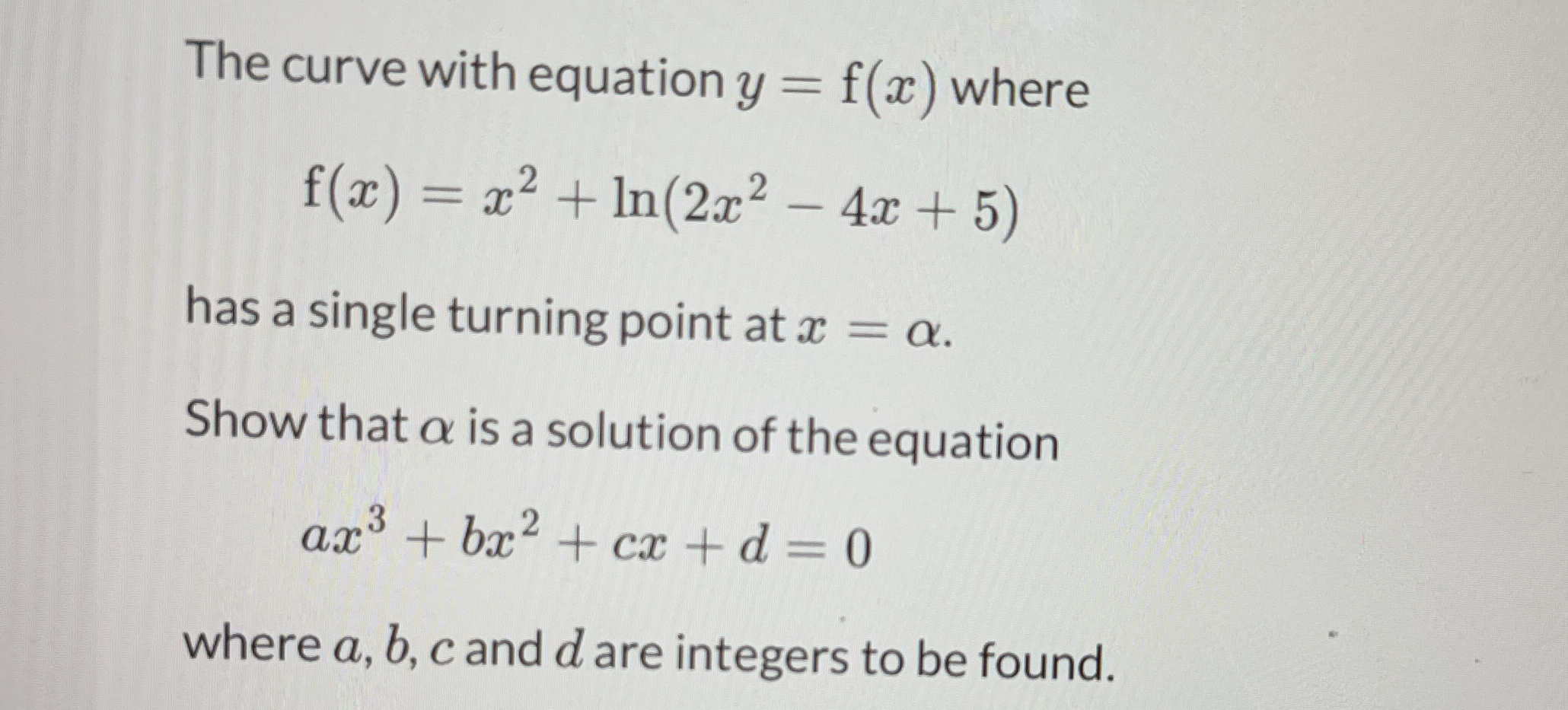
Understand the Problem
The question asks us to demonstrate that a certain variable (α) is a solution to a polynomial equation given that the function f(x) has a specific turning point. This involves deriving the function, identifying conditions of a single turning point, and establishing the relationship with the polynomial.
Answer
The coefficients found are \( a = 4 \), \( b = -8 \), \( c = 10 \), \( d = 4 \). Thus, \( \alpha \) satisfies \( 4\alpha^3 - 8\alpha^2 + 10\alpha + 4 = 0 \).
Answer for screen readers
The coefficients are $a = 4$, $b = -8$, $c = 10$, and $d = 4$. Therefore, ( \alpha ) is a solution of the equation:
$$ 4\alpha^3 - 8\alpha^2 + 10\alpha + 4 = 0 $$
Steps to Solve
- Differentiate the function
To find the turning points, we need the first derivative of the function $f(x)$.
$$ f'(x) = \frac{d}{dx} \left( x^2 + \ln(2x^2 - 4x + 5) \right) $$
Using the derivative rules:
$$ f'(x) = 2x + \frac{1}{2x^2 - 4x + 5} \cdot (4x - 4) $$
This provides the expression for the derivative.
- Set the derivative to zero
For a turning point at $x = \alpha$, we set $f'(\alpha) = 0$:
$$ 2\alpha + \frac{4(\alpha - 1)}{2\alpha^2 - 4\alpha + 5} = 0 $$
This equation will help us find the value of $\alpha$.
- Find simplified form from turning point condition
Rearranging gives us:
$$ 2\alpha(2\alpha^2 - 4\alpha + 5) + 4(\alpha - 1) = 0 $$
Expand this to get a polynomial in $\alpha$.
- Formulate the polynomial equation
Visibly expanding the terms together leads to:
$$ 4\alpha^3 - 8\alpha^2 + 10\alpha + 4 = 0 $$
This is now in the form of $a\alpha^3 + b\alpha^2 + c\alpha + d = 0$.
- Identify coefficients a, b, c, and d
From $4\alpha^3 - 8\alpha^2 + 10\alpha + 4 = 0$, we can directly identify:
- $a = 4$
- $b = -8$
- $c = 10$
- $d = 4$
The coefficients are $a = 4$, $b = -8$, $c = 10$, and $d = 4$. Therefore, ( \alpha ) is a solution of the equation:
$$ 4\alpha^3 - 8\alpha^2 + 10\alpha + 4 = 0 $$
More Information
This polynomial was derived from the properties of the function concerning its derivative, affirming that $f(x)$ has a single turning point at $x = \alpha$.
Tips
- Forgetting to apply the chain rule while differentiating logarithmic functions.
- Not simplifying the equation after setting the derivative to zero.
- Misidentifying the coefficients in the polynomial form.
AI-generated content may contain errors. Please verify critical information