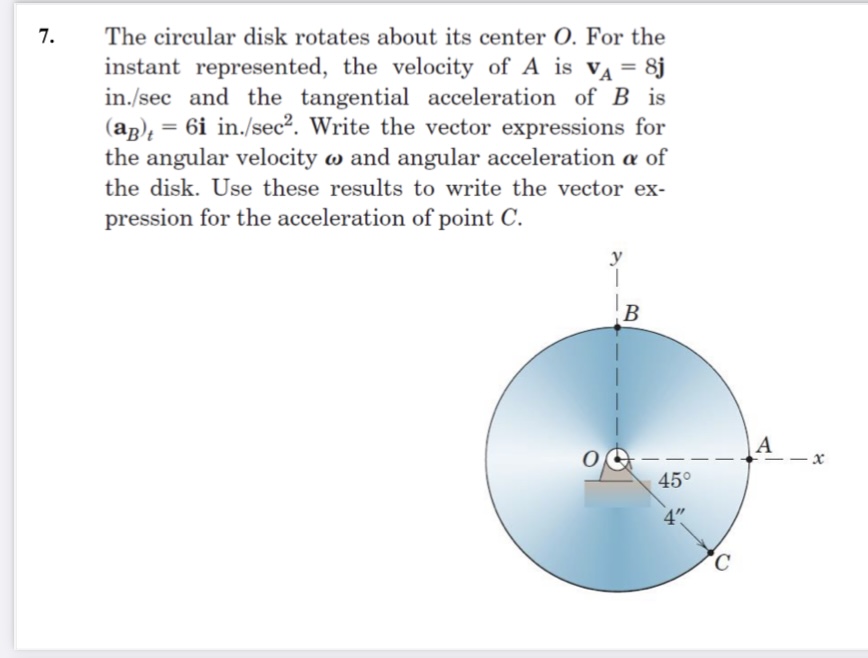
The circular disk rotates about its center O. For the instant represented, the velocity of A is vA = 8j in./sec and the tangential acceleration of B is aBt = 6i in./sec². Write the... The circular disk rotates about its center O. For the instant represented, the velocity of A is vA = 8j in./sec and the tangential acceleration of B is aBt = 6i in./sec². Write the vector expressions for the angular velocity ω and angular acceleration α of the disk. Use these results to write the vector expression for the acceleration of point C. Read more

Steps to Solve

1. Identify angular velocity ($\omega$)

Given the velocity of point A, $v_A = 8 , \mathbf{j} , \text{in/sec}$, we can express it in terms of angular velocity. The position vector of point A is $\mathbf{r}_A = 4 , \mathbf{i} + 4 , \mathbf{j}$.

Using the relationship for linear velocity: $$ \mathbf{v} = \mathbf{\omega} \times \mathbf{r} $$

Assuming $\omega$ is in the $k$ direction (out of the plane), we have: $$ \mathbf{v}_A = \omega \cdot \mathbf{r}_A = \omega \begin{bmatrix} 0 \ 0 \ 1 \end{bmatrix} \times \begin{bmatrix} 4 \ 4 \ 0 \end{bmatrix} = \begin{bmatrix} -4\omega \ 4\omega \ 0 \end{bmatrix} $$

Since $v_A = 8 , \mathbf{j}$, we can equate components: $$ 4\omega = 8 \implies \omega = 2 , \text{rad/sec} $$

2. Identify angular acceleration ($\alpha$)

The tangential acceleration of point B is given as $a_{B_t} = 6 , \mathbf{i} , \text{in/sec}^2$. This relates to the angular acceleration as: $$ a_{t} = \alpha r $$

Where $r$ is the distance from the center to point B, which is 4 inches. Therefore: $$ 6 = \alpha \cdot 4 \implies \alpha = \frac{6}{4} = 1.5 , \text{rad/sec}^2 $$

3. Write the vector expressions for angular velocity and angular acceleration

The vector expression for angular velocity $\omega$ is: $$ \mathbf{\omega} = 2 , \mathbf{k} , \text{rad/sec} $$

The vector expression for angular acceleration $\alpha$ is: $$ \mathbf{\alpha} = 1.5 , \mathbf{k} , \text{rad/sec}^2 $$

4. Determine the acceleration of point C

The acceleration of point C, $\mathbf{a_C}$, has two components: tangential acceleration $\mathbf{a_t}$ and centripetal acceleration $\mathbf{a_c}$.

• Tangential acceleration: $$ \mathbf{a_t} = \alpha \cdot r_C $$ where $r_C = 4 \text{ in} \cdot \cos(45^\circ) + 4 \text{ in} \cdot \sin(45^\circ) = 4 \in , \sqrt{2}$. Thus, $$ \mathbf{a_t} = 1.5 \cdot (4\sqrt{2}) = 6\sqrt{2} , \mathbf{j} , \text{in/sec}^2 $$

• Centripetal acceleration: $$ \mathbf{a_c} = \omega^2 r_C $$ Calculating for $r_C = 4\sqrt{2}$: $$ \mathbf{a_c} = 2^2 (4\sqrt{2}) = 16 , \mathbf{k} , \text{in/sec}^2 $$

Adding both components gives: $$ \mathbf{a_C} = \mathbf{a_t} + \mathbf{a_c} = 6\sqrt{2} , \mathbf{j} + 16 , \mathbf{k} , \text{in/sec}^2 $$