The characteristic equation of the matrix A = [1 0 0; 1 0 1; 0 1 0] is which of the following? A. -λ^3 + λ^2 + λ - 1 = 0 B. -λ^3 + λ^2 - λ - 1 = 0 C. -λ^3 - λ^2 + λ - 1 = 0 D. -λ^3... The characteristic equation of the matrix A = [1 0 0; 1 0 1; 0 1 0] is which of the following? A. -λ^3 + λ^2 + λ - 1 = 0 B. -λ^3 + λ^2 - λ - 1 = 0 C. -λ^3 - λ^2 + λ - 1 = 0 D. -λ^3 + λ^2 + λ + 1 = 0.
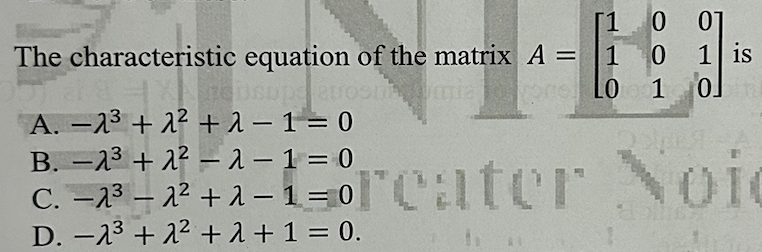
Understand the Problem
The question is asking for the characteristic equation of the given matrix A. We need to determine which of the provided options correctly represents this equation.
Answer
The characteristic equation is $-\lambda^3 + \lambda^2 + \lambda - 1 = 0$.
Answer for screen readers
The characteristic equation of the matrix $A$ is given by:
$$ -\lambda^3 + \lambda^2 + \lambda - 1 = 0 $$
Steps to Solve
- Find the Characteristic Polynomial
To find the characteristic equation, we calculate the determinant of the matrix $A - \lambda I$, where $I$ is the identity matrix and $\lambda$ is a scalar. For the given matrix $A = \begin{bmatrix} 1 & 0 & 0 \ 1 & 0 & 1 \ 0 & 1 & 0 \end{bmatrix}$, we have:
$$ A - \lambda I = \begin{bmatrix} 1 - \lambda & 0 & 0 \ 1 & 0 - \lambda & 1 \ 0 & 1 & 0 - \lambda \end{bmatrix} $$
- Calculate the Determinant
Next, we calculate the determinant of the matrix from the previous step:
$$ \text{det}(A - \lambda I) = \begin{vmatrix} 1 - \lambda & 0 & 0 \ 1 & -\lambda & 1 \ 0 & 1 & -\lambda \end{vmatrix} $$
Using the determinant formula for a $3 \times 3$ matrix, we can expand this:
$$ = (1 - \lambda) \begin{vmatrix} -\lambda & 1 \ 1 & -\lambda \end{vmatrix} $$
- Calculate the $2 \times 2$ Determinant
The determinant of the $2 \times 2$ matrix is:
$$ = (-\lambda)(-\lambda) - (1)(1) = \lambda^2 - 1 $$
So now we have:
$$ \text{det}(A - \lambda I) = (1 - \lambda)(\lambda^2 - 1) $$
- Simplify the Determinant Expression
We now expand this:
$$ = (1 - \lambda)(\lambda - 1)(\lambda + 1) $$
- Set the Characteristic Equation
Finally, to find the characteristic polynomial, we set the determinant equal to zero:
$$ (1 - \lambda)(\lambda - 1)(\lambda + 1) = 0 $$
This leads to:
$$ -\lambda^3 + \lambda^2 + \lambda - 1 = 0 $$
The characteristic equation of the matrix $A$ is given by:
$$ -\lambda^3 + \lambda^2 + \lambda - 1 = 0 $$
More Information
The characteristic equation is crucial for finding the eigenvalues of the matrix, which are important in various applications like stability analysis and systems of differential equations. This equation represents a polynomial whose roots correspond to the eigenvalues of matrix $A$.
Tips
- Not accounting for the correct sign when expanding determinants can lead to incorrect characteristic equations. Always verify the signs during expansion.
- Forgetting to set the determinant equal to zero to find the characteristic equation can result in missing solutions.
AI-generated content may contain errors. Please verify critical information