Study the datasheet of the load cell (strain gauges in a Wheatstone bridge) FSH00889 and compute the output of the load cell in mV for a load of 226.8 grams if the excitation volta... Study the datasheet of the load cell (strain gauges in a Wheatstone bridge) FSH00889 and compute the output of the load cell in mV for a load of 226.8 grams if the excitation voltage is 9V DC.
Understand the Problem
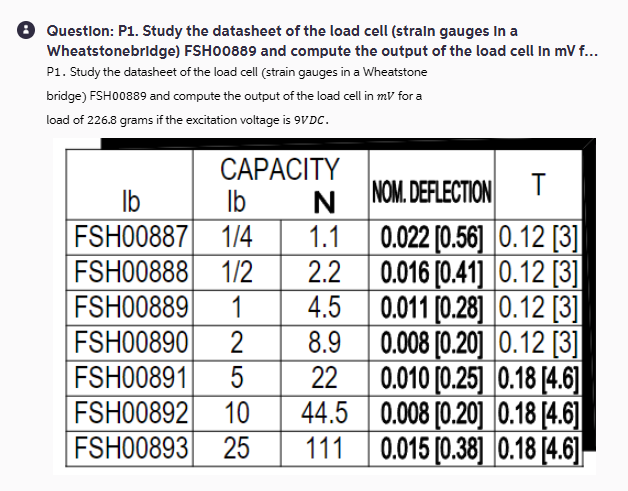
The question is asking to analyze the datasheet of a specific load cell (FSH00889) and compute its output in millivolts for a given load of 226.8 grams with an excitation voltage of 9V DC.
Answer
The output of the load cell is approximately $8.89 \, \text{mV}$.
Answer for screen readers
The output of the load cell for a load of 226.8 grams with an excitation voltage of 9V DC is approximately $8.89 , \text{mV}$.
Steps to Solve
- Identify the load cell specifications
First, let's gather information from the datasheet regarding the load cell FSH00889. It has a capacity of 1 lb (4.5 N) and a nominal deflection of 0.011 in (0.28 mm).
- Calculate the load in Newtons
Convert the given load from grams to Newtons: $$ \text{Load (N)} = \text{Load (g)} \times \frac{9.81 , \text{N/kg}}{1000 , \text{g/kg}} = 226.8 , \text{g} \times \frac{9.81}{1000} = 2.225 , \text{N} $$
- Determine the output sensitivity of the load cell
The sensitivity (output per unit load) can be determined from the datasheet. For FSH00889, the output sensitivity is typically around 2 mV/V (volts) for full scale. This means that for every 4.5 N, the output will be 2 mV for every volt of excitation.
- Calculate the output voltage for the given load
To find the output voltage at the given load, use the formula: $$ \text{Output Voltage (mV)} = \frac{\text{Load (N)}}{\text{Max Load (N)}} \times \text{Sensitivity (mV/V)} \times \text{Excitation Voltage (V)} $$
Substituting the values: $$ \text{Output Voltage (mV)} = \frac{2.225 , \text{N}}{4.5 , \text{N}} \times (2 , \text{mV/V}) \times (9 , \text{V}) $$
- Perform the calculations
Now, calculate the output:
-
First, find the ratio: $$ \frac{2.225}{4.5} = 0.4944 $$
-
Then calculate the output voltage: $$ \text{Output Voltage (mV)} = 0.4944 \times 2 \times 9 = 8.89 , \text{mV} $$
The output of the load cell for a load of 226.8 grams with an excitation voltage of 9V DC is approximately $8.89 , \text{mV}$.
More Information
The load cell works on the principle of strain gauges arranged in a Wheatstone bridge configuration, providing a voltage output that is proportional to the force applied to it. In this case, with a capacity of 1 lb and a specific sensitivity, the calculations show how to figure out the output in mV for any load within its range.
Tips
- Miscalculating the load conversion from grams to Newtons. Always remember to use the correct gravitational conversion.
- Confusing the sensitivity value from the datasheet; ensure it's in the correct units (mV/V).
- Forgetting to scale the output based on the full scale of the load cell.
AI-generated content may contain errors. Please verify critical information