Solve: x^3 + 3xy^2 = 14, y^3 + 3x^2y = -13
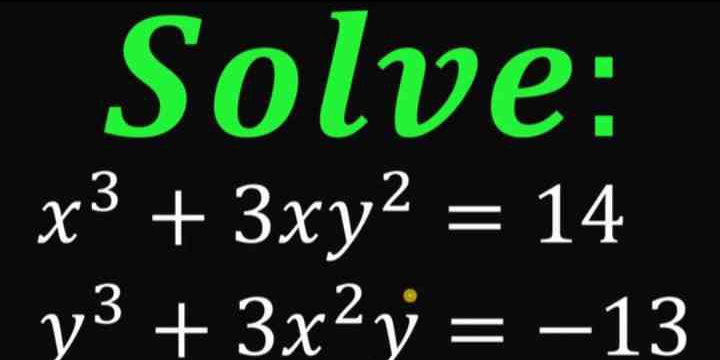
Understand the Problem
The question is asking us to solve a system of two equations involving variables x and y. Specifically, we need to find the values of x and y that satisfy both equations simultaneously.
Answer
$(x, y) = (2, -1)$
Answer for screen readers
The solution to the system of equations is $(x, y) = (2, -1)$.
Steps to Solve
-
Identify the equations to solve We have the following system of equations: $$ x^3 + 3xy^2 = 14 $$ $$ y^3 + 3x^2y = -13 $$
-
Rearranging the equations Let's rearrange the first equation for $x^3$: $$ x^3 = 14 - 3xy^2 $$
-
Substituting into the second equation Now substitute $x^3$ into the second equation. We replace $y^3$: $$ y^3 = -13 - 3x^2y $$
-
Exploring potential solutions Since the equations are symmetric in form, we can test integer values for $x$ and $y$. Testing $(x, y) = (2, -1)$:
-
For $x = 2, y = -1$: $$ x^3 + 3xy^2 = 2^3 + 3(2)(-1)^2 = 8 + 6 = 14 $$ This holds true.
-
Now check the second equation: $$ y^3 + 3x^2y = (-1)^3 + 3(2)^2(-1) = -1 - 12 = -13 $$ This also holds true.
-
-
Conclusion with solutions Thus, we conclude that the solution to the system is: $$ (x, y) = (2, -1) $$
The solution to the system of equations is $(x, y) = (2, -1)$.
More Information
These equations represent a system with symmetry in cubic forms. The solution found, $(2, -1)$, satisfies both equations.
Tips
- Not checking for all potential integer solutions can lead to missing valid pairs.
- Only substituting in one equation instead of both can result in incorrect conclusions.
AI-generated content may contain errors. Please verify critical information