Solve using substitution. -3x - 7y = 8; -x - 5y = 16

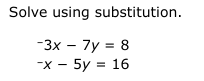
Understand the Problem

The question is asking to solve a system of equations using the substitution method. This involves isolating one variable in one equation and substituting it into the other equation to find the values of both variables.

Answer

The solution is $ x = 9 $ and $ y = -5 $.

Steps to Solve

Isolate one variable

Let's isolate $x$ in the second equation: $$ -x - 5y = 16 $$ Rearranging gives: $$ -x = 16 + 5y $$ Thus, $$ x = -16 - 5y $$

Substitute into the first equation

Now we'll substitute $x$ into the first equation: $$ -3x - 7y = 8 $$ Replacing $x$ gives: $$ -3(-16 - 5y) - 7y = 8 $$

Simplify the equation

Distributing $-3$: $$ 48 + 15y - 7y = 8 $$ Combine like terms: $$ 48 + 8y = 8 $$

Solve for $y$

Now, isolate $y$ by subtracting 48 from both sides: $$ 8y = 8 - 48 $$ $$ 8y = -40 $$ Dividing by 8 gives: $$ y = -5 $$

Substitute back to find $x$

Now substitute $y$ back into the expression we found for $x$: $$ x = -16 - 5(-5) $$ This simplifies to: $$ x = -16 + 25 $$ Thus, $$ x = 9 $$

The solution to the system of equations is ( x = 9 ) and ( y = -5 ).

More Information

This solution gives the values of ( x ) and ( y ) where both equations intersect. Solving systems of equations using substitution is a useful technique, especially when one equation easily allows for isolation of a variable.

Tips

Forgetting to distribute or combine like terms correctly during simplification can lead to incorrect values.
Failing to substitute the variable back into the correct equation can lead to erroneous results.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!