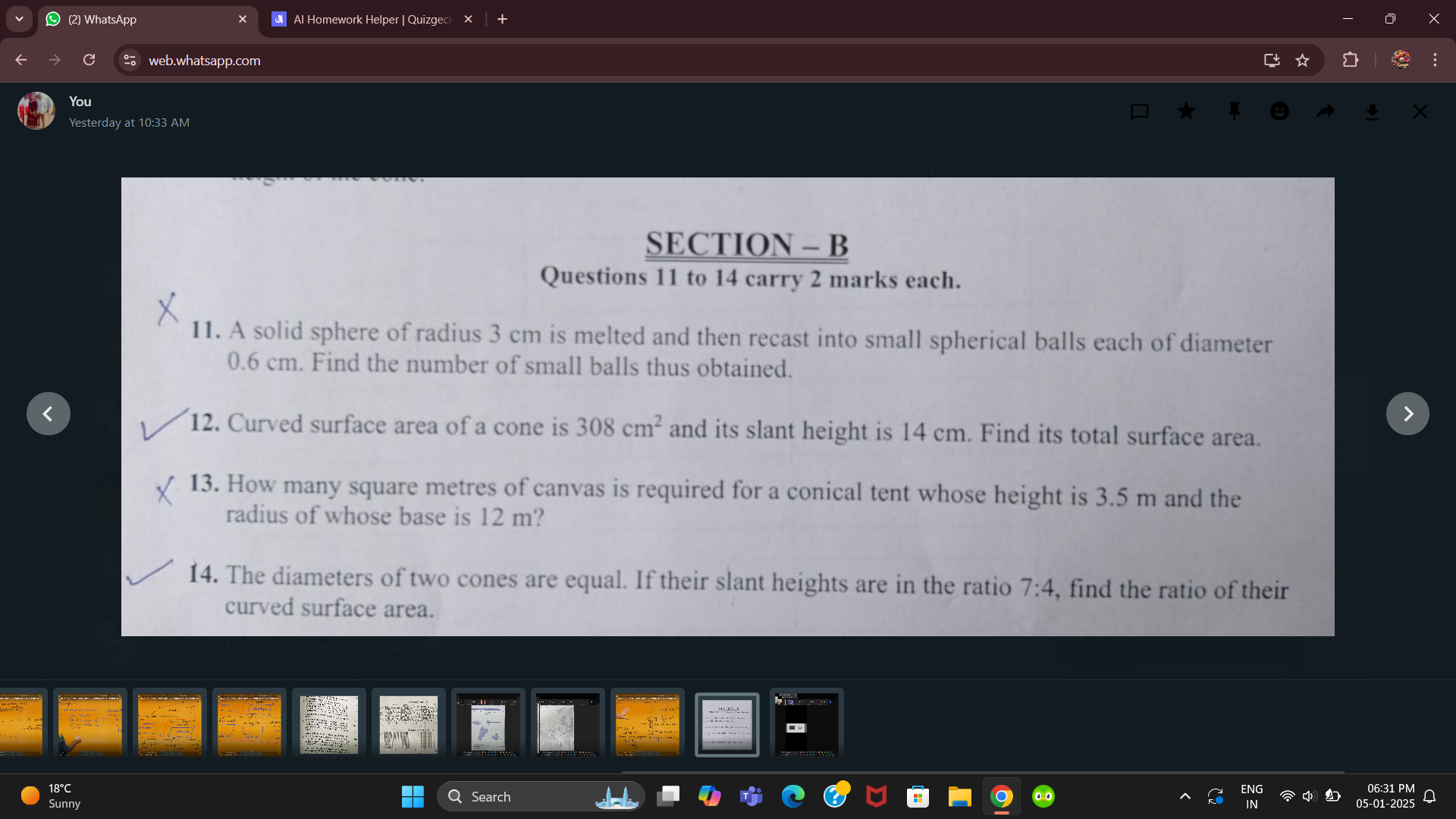
A solid sphere of radius 3 cm is melted and then recast into small spherical balls each of diameter 0.6 cm. Find the number of small balls thus obtained. Curved surface area of a c... A solid sphere of radius 3 cm is melted and then recast into small spherical balls each of diameter 0.6 cm. Find the number of small balls thus obtained. Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find its total surface area. How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of whose base is 12 m? The diameters of two cones are equal. If their slant heights are in the ratio 7:4, find the ratio of their curved surface area. Read more

Steps to Solve

1. Calculate the Volume of the Large Sphere

The volume $V$ of a sphere is given by the formula:

$$ V = \frac{4}{3} \pi r^3 $$

For the large sphere with radius $r = 3$ cm:

$$ V = \frac{4}{3} \pi (3)^3 = \frac{4}{3} \pi (27) = 36\pi , \text{cm}^3 $$

2. Calculate the Volume of One Small Sphere

The radius of each small sphere is given by the diameter of $0.6$ cm. Thus, the radius is:

$$ r = \frac{0.6}{2} = 0.3 , \text{cm} $$

The volume of the small sphere is:

$$ V_{small} = \frac{4}{3} \pi (0.3)^3 = \frac{4}{3} \pi (0.027) = 0.036\pi , \text{cm}^3 $$

3. Determine the Number of Small Spheres

To find the number of small spheres, divide the volume of the large sphere by the volume of one small sphere:

$$ N = \frac{V_{large}}{V_{small}} = \frac{36\pi}{0.036\pi} = 1000 $$

4. Calculate Total Surface Area of the Cone

The curved surface area (CSA) of the cone is given as $308 , \text{cm}^2$. The total surface area (TSA) of a cone is:

$$ TSA = CSA + \text{Base Area} $$

The base area can be calculated using the formula for the area of a circle, where the base radius can be found from the slant height and height.

Using the relationship between radius, height, and slant height:

$$ h = \sqrt{l^2 - r^2} $$

Given the slant height ($l = 14$ cm), we need to find the base radius from the curved surface area which is:

$$ CSA = \pi r l $$

Using the CSA:

$$ 308 = \pi r (14) \Rightarrow r = \frac{308}{14\pi} $$

Now find the base area and add to CSA for TSA.

5. Calculate the Canvas Required for the Conical Tent

The formula for the curved surface area of a cone is:

$$ CSA = \pi r l $$

where $r = 12$ m and $h = 3.5$ m. To find the slant height:

$$ l = \sqrt{r^2 + h^2} = \sqrt{(12)^2 + (3.5)^2} = \sqrt{144 + 12.25} = \sqrt{156.25} = 12.5, m $$

Now calculate the CSA:

$$ CSA = \pi (12)(12.5) $$

6. Calculate the Ratio of Curved Surface Areas of Two Cones

Since the diameters are equal, we will find the ratio of the curved surface areas using the slant heights in the ratio $7:4$:

The formula for the curved surface area remains:

$$ \text{CSA}{1} : \text{CSA}{2} = \frac{l_1}{l_2} = \frac{7}{4} $$

Thus, the ratio of their curved surface areas is also $7:4$.