Solve the system of linear equations by graphing: y = -4x + 3 and 4x - 2y = 6.

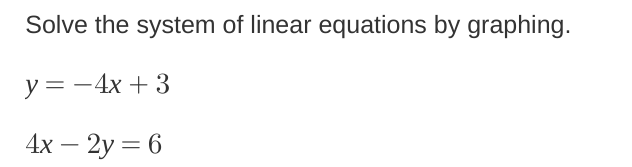
Understand the Problem

The question asks to solve a system of linear equations by graphing. It involves two equations: one in slope-intercept form and the other in standard form, which may need to be converted to slope-intercept form for graphing.

Answer

The solution is $ (1, -1) $.

Steps to Solve

Graph the first equation

The first equation is already in slope-intercept form: $$ y = -4x + 3 $$

The slope (m) is -4 and the y-intercept (b) is 3.
Plot the y-intercept (0, 3) on the graph.
From the y-intercept, use the slope to find another point: down 4 units and right 1 unit to (1, -1).
Draw the line through these points.

Convert and graph the second equation

The second equation is in standard form: $$ 4x - 2y = 6 $$

To convert it to slope-intercept form, solve for y: $$ -2y = -4x + 6 $$ $$ y = 2x - 3 $$
Now, the slope (m) is 2 and the y-intercept (b) is -3.
Plot the y-intercept (0, -3) on the graph.
From this point, use the slope to find another point: up 2 units and right 1 unit to (1, -1).
Draw the line through these points.

Identify the intersection point

After graphing both lines, observe where they intersect. The coordinates of the intersection point represent the solution to the system of equations.

The solution to the system of equations is the point of intersection: ( (1, -1) ).

More Information

The solution ( (1, -1) ) means that when both equations are satisfied, the values of x and y are 1 and -1 respectively. This point is where both lines meet on the graph.

Tips

Incorrect plotting: Ensure you accurately plot the points based on the slopes and intercepts.
Miscalculating slopes: Double-check calculations when determining the slope and converting to slope-intercept form.
Ignoring the graph scale: Ensure that the graph is properly scaled to clearly see the intersection.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!