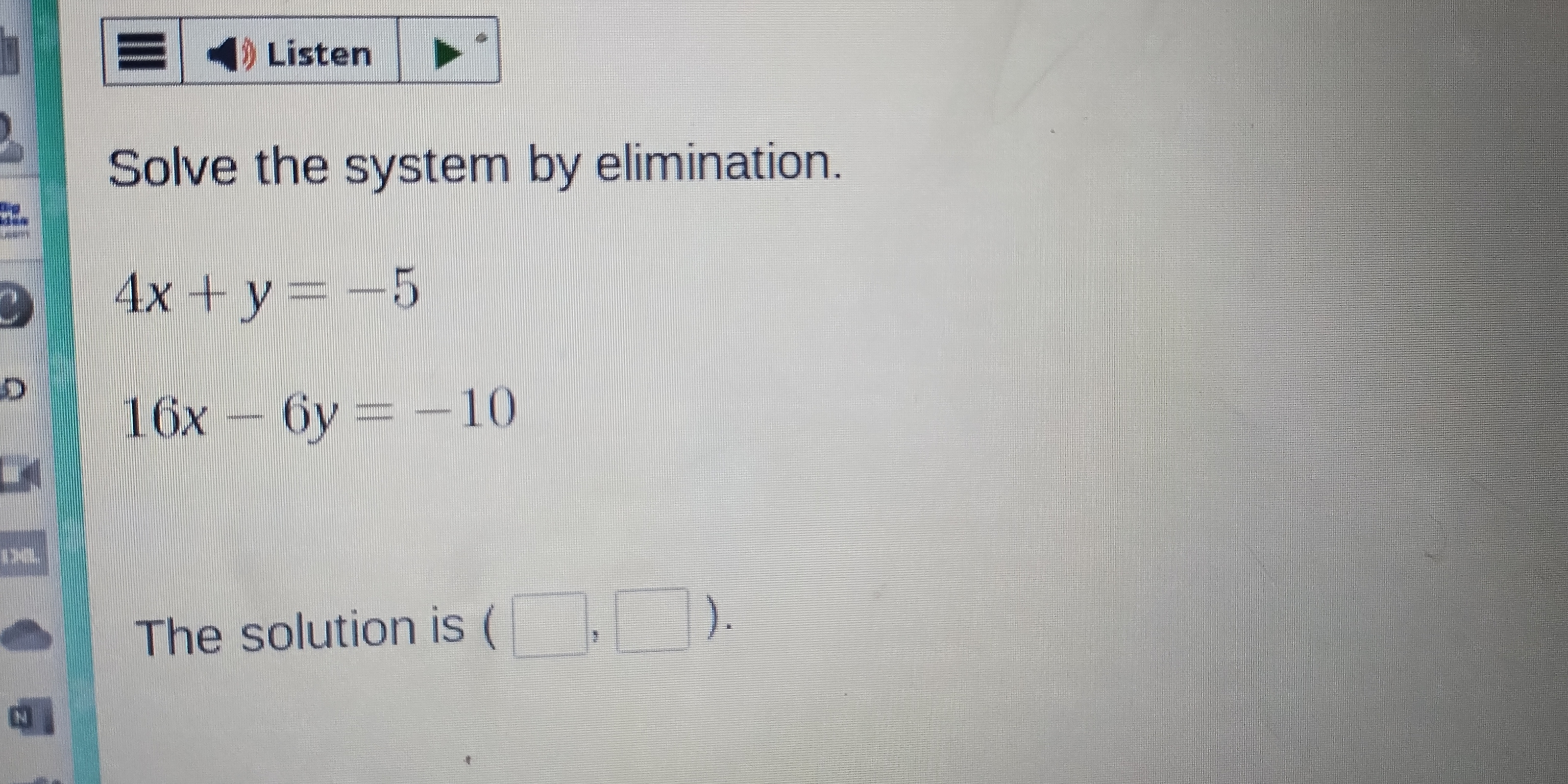
Solve the system by elimination. 4x + y = -5 16x - 6y = -10 The solution is ( , ).
Understand the Problem
The question is asking to solve a system of equations using the elimination method. The user wants to find the values of x and y that satisfy both equations simultaneously.
Answer
The solution is $(-1, -1)$.
Answer for screen readers
The solution is $(-1, -1)$.
Steps to Solve
-
Align the Equations
We have two equations:
$$ 4x + y = -5 $$
$$ 16x - 6y = -10 $$ -
Multiply the First Equation
To eliminate $y$, let's manipulate the first equation by multiplying it by 6:
$$ 6(4x + y) = 6(-5) $$
This gives:
$$ 24x + 6y = -30 $$ -
Set Up for Elimination
Now we can set up the system for elimination:- New Equation 1: $$ 24x + 6y = -30 $$
- Equation 2 remains: $$ 16x - 6y = -10 $$
-
Add the Two Equations
Now we can add the two equations together to eliminate $y$:
$$ (24x + 6y) + (16x - 6y) = -30 - 10 $$
This simplifies to:
$$ 40x = -40 $$ -
Solve for x
Now we can solve for $x$:
$$ x = \frac{-40}{40} = -1 $$ -
Substitute x Back into One of the Original Equations
Substitute $x = -1$ into the first equation to find $y$:
$$ 4(-1) + y = -5 $$
This simplifies to:
$$ -4 + y = -5 $$ -
Solve for y
Solving for $y$ gives:
$$ y = -5 + 4 = -1 $$
The solution is $(-1, -1)$.
More Information
The solution $(-1, -1)$ means that the two original equations intersect at the point where both $x$ and $y$ equal -1. This point satisfies both equations simultaneously.
Tips
- Forgetting to multiply both sides of the equation when you scale an equation.
- Not aligning equations properly before elimination, which can cause confusion.
- Mixing up signs when adding equations, leading to incorrect results.
AI-generated content may contain errors. Please verify critical information