Solve the following quadratic equation for all values of x in simplest form: 5(x² - 8) - 5 = 5.
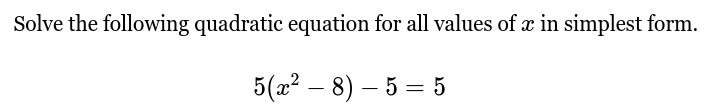
Understand the Problem
The question is asking to solve a given quadratic equation for all values of x and express the solution in its simplest form. The equation provided is 5(x² - 8) - 5 = 5.
Answer
The solutions are \( x = \sqrt{10} \) and \( x = -\sqrt{10} \).
Answer for screen readers
The solutions are ( x = \sqrt{10} ) and ( x = -\sqrt{10} ).
Steps to Solve
-
Distribute the 5 on the left side
Start by distributing the 5 into the parenthesis:
$$ 5(x^2 - 8) = 5x^2 - 40 $$
The equation becomes:
$$ 5x^2 - 40 - 5 = 5 $$
-
Simplify the left side
Combine like terms on the left side:
$$ 5x^2 - 45 = 5 $$
-
Isolate the quadratic term
Add 45 to both sides of the equation to isolate the quadratic term:
$$ 5x^2 = 50 $$
-
Divide by 5
To solve for $x^2$, divide both sides by 5:
$$ x^2 = 10 $$
-
Take the square root
Take the square root of both sides to solve for $x$:
$$ x = \pm \sqrt{10} $$
The solutions are ( x = \sqrt{10} ) and ( x = -\sqrt{10} ).
More Information
This problem illustrates how to solve a quadratic equation by isolating the variable and using the properties of square roots. The solutions indicate two possible values for ( x ).
Tips
- Forgetting to consider both the positive and negative square roots when solving for ( x ). Always remember that taking the square root of a number can yield two values.
AI-generated content may contain errors. Please verify critical information