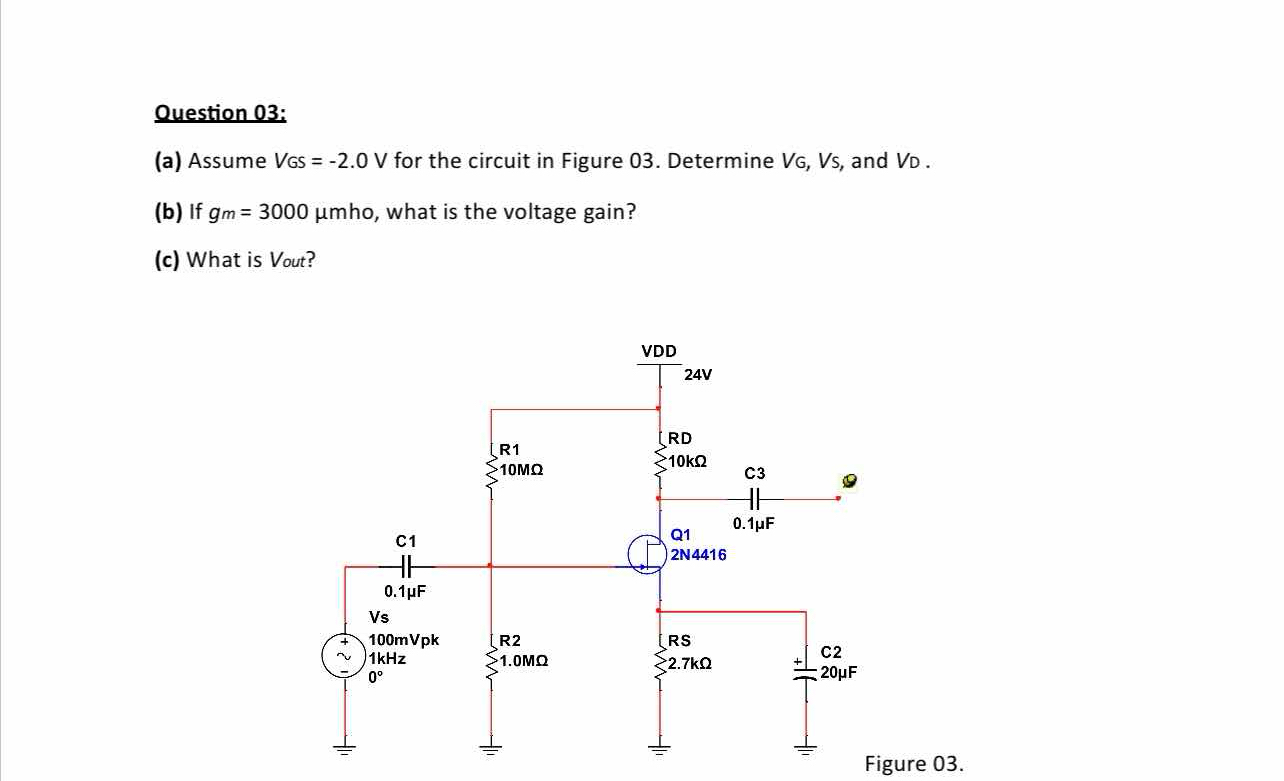
Assume VGS = -2.0 V for the circuit in Figure 03. Determine VG, VS, and VD. If gm = 3000 µmho, what is the voltage gain? What is Vout?

Steps to Solve

1. Determine $V_G$, $V_S$, and $V_D$

   Given that $V_{GS} = -2.0 , V$, the gate voltage $V_G$ can be defined. Since $V_G$ is the bias voltage set by the input network, we can assume it to be zero in this analysis.

   The source voltage $V_S$ is given by:

   $$ V_S = V_G - V_{GS} $$

   Substituting $V_G = 0 , V$ and $V_{GS} = -2.0 , V$:

   $$ V_S = 0 - (-2.0) = 2.0 , V $$

   The drain voltage $V_D$ can be computed from the power supply voltage and the voltage drop across $R_D$:

   $$ V_D = V_{DD} - I_D \cdot R_D $$

   To find $I_D$, we can use Ohm’s Law, considering the drain current $I_D$ passes through the resistor $R_D$.

2. Calculate $I_D$ and $V_D$

   Note: Calculate $I_D$ based on the small-signal model. Since $R_S = 2.7 , k\Omega$:

   $$ I_D \approx \frac{V_S}{R_S} = \frac{2.0 , V}{2700 , \Omega} \approx 0.74 , mA $$

   Now, substituting $I_D$ into the equation for $V_D$:

   $$ V_D = 24 , V - (0.74 \times 10^{-3} , A) \cdot 10 , k\Omega \approx 24 - 7.4 \approx 16.6 , V $$

3. Calculate Voltage Gain ($A_V$)

   The voltage gain can be defined using the transconductance $g_m$:

   $$ A_V = -g_m \cdot \frac{R_D}{R_S} $$

   Given $g_m = 3000 , \mu mho = 3 , mS$:

   $$ A_V = -3 , mS \cdot \frac{10, k\Omega}{2.7 , k\Omega} $$

   Simplifying this:

   $$ A_V = -3 \times \frac{10}{2.7} = -11.11 $$

4. Calculate Output Voltage ($V_{out}$)

   The output voltage can be calculated using the formula for the output voltage given the voltage gain and input voltage:

   $$ V_{out} = A_V \cdot V_{in} $$

   The input voltage $V_{in}$ is given as $100 , mVp$ or $0.1 , V$. Therefore:

   $$ V_{out} = -11.11 \cdot 0.1 = -1.111 , V $$