Solve the following differential equation: (x^2 + y^2)(dx + 2y dy) = 0.
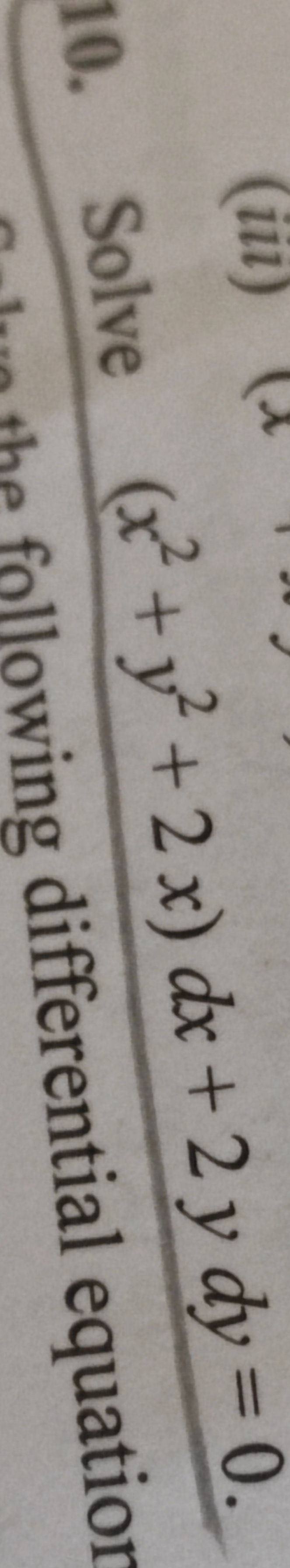
Understand the Problem
The question is asking to solve a given differential equation involving both x and y, specifically the equation (x^2 + y^2)(dx + 2y dy) = 0.
Answer
The solution is $x + y^2 = C$.
Answer for screen readers
The solution to the differential equation is:
$$x + y^2 = C,$$
where $C$ is a constant.
Steps to Solve
-
Factor the equation
Begin with the equation:
$$(x^2 + y^2)(dx + 2y, dy) = 0.$$
This means either $x^2 + y^2 = 0$ or $dx + 2y, dy = 0$. -
Solve the first part: $x^2 + y^2 = 0$
The equation $x^2 + y^2 = 0$ has only one solution, which is $x = 0$ and $y = 0$. This represents a specific point. -
Solve the second part: $dx + 2y, dy = 0$
Rearrange the equation:
$$dx = -2y, dy.$$
Now, separate the variables:
$$\frac{dx}{dy} = -2y.$$ -
Integrate both sides
Integrate the left side with respect to $x$ and the right side with respect to $y$:
$$\int dx = -2 \int y, dy.$$
This results in:
$$x = -y^2 + C,$$
where $C$ is the constant of integration. -
Final equation
The final implicit solution to the differential equation is:
$$x + y^2 = C.$$
The solution to the differential equation is:
$$x + y^2 = C,$$
where $C$ is a constant.
More Information
This equation represents a family of parabolas in the xy-plane. Each value of $C$ gives a different curve, illustrating how $x$ and $y$ are related.
Tips
- Incorrectly assuming $x^2 + y^2 = 0$ has solutions other than $(0, 0)$.
- Misunderstanding the separation of variables, leading to errors in integration.
AI-generated content may contain errors. Please verify critical information