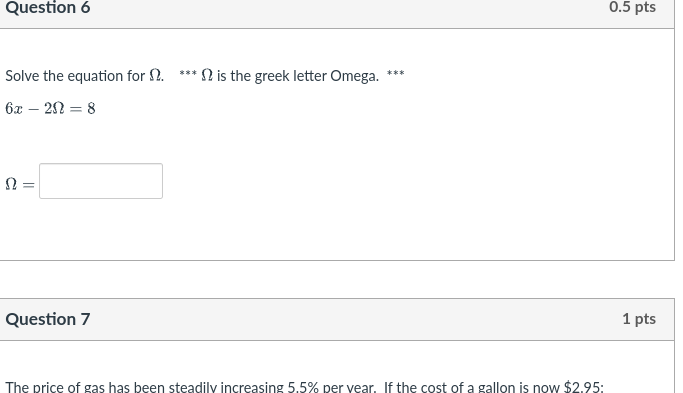
Solve the equation for Ω: 6x - 2Ω = 8.
Understand the Problem
The question is asking to solve an equation involving the Greek letter Omega (Ω). Specifically, we need to find the value of Ω in the equation 6x - 2Ω = 8.
Answer
$$ Ω = 3x - 4 $$
Answer for screen readers
$$ Ω = 3x - 4 $$
Steps to Solve
- Rearranging the Equation
We start with the equation:
$$ 6x - 2Ω = 8 $$
We want to isolate the term involving Ω. First, we'll move ( 6x ) to the other side:
$$ -2Ω = 8 - 6x $$
- Dividing by -2
Next, we need to solve for Ω by dividing both sides by -2:
$$ Ω = \frac{8 - 6x}{-2} $$
- Simplifying the Expression
To simplify, we can separate the terms in the numerator:
$$ Ω = \frac{8}{-2} - \frac{6x}{-2} $$
This gives us:
$$ Ω = -4 + 3x $$
- Final Expression for Ω
Thus, our final expression for Ω is:
$$ Ω = 3x - 4 $$
$$ Ω = 3x - 4 $$
More Information
The equation ( 6x - 2Ω = 8 ) can be solved to express Ω in terms of x. This simple linear equation illustrates basic algebraic manipulation, including rearranging terms and simplifying fractions.
Tips
- Not distributing correctly when dividing the entire expression by -2.
- Forgetting to change the signs when moving terms from one side of the equation to the other.
AI-generated content may contain errors. Please verify critical information