Solve \( \frac{\partial^3 z}{\partial x^3} - 2 \frac{\partial^3 z}{\partial x^2 \partial y} = 2e^{2x} + 3x^2 y . \)
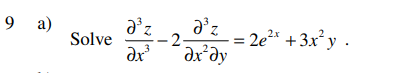
Understand the Problem
The question is asking to solve a partial differential equation involving third partial derivatives of a function z with respect to x and y. The equation given is a linear combination of these derivatives equal to a function of x and y.
Answer
$$ z(x, y) = \frac{1}{4} e^{2x} + \frac{C_1}{2} x^2 + C_2 x - \frac{3}{4} y^2 + C_3 $$
Answer for screen readers
The general solution is: $$ z(x, y) = \frac{1}{4} e^{2x} + \frac{C_1}{2} x^2 + C_2 x - \frac{3}{4} y^2 + C_3 $$
Steps to Solve
- Identify the Form of the Solution
We start by noting that the equation we need to solve involves third partial derivatives. A common technique is to assume a solution of the form: $$ z(x, y) = f(x) + g(y) $$
- Take the Required Derivatives
We need to compute the required derivatives of ( z ):
-
The third derivative with respect to ( x ): $$ \frac{\partial^3 z}{\partial x^3} = f'''(x) $$
-
The mixed third derivative: $$ \frac{\partial^3 z}{\partial x^2 \partial y} = f''(x) g'(y) $$
- Substitute Derivatives into the Equation
Now we substitute these derivatives back into the original equation: $$ f'''(x) - 2 f''(x) g'(y) = 2e^{2x} + 3x^2y $$
- Separate the Variables
This will give us two parts, one dependent on ( x ) and the other on ( y ). We can rearrange to isolate terms involving ( x ): $$ f'''(x) - 2 f''(x) g'(y) = 2e^{2x} + 3x^2y $$
- Equate the Parts
To satisfy this equation for all ( x ) and ( y ), we need to set the ( y ) component equal to ( 0 ) leading to: $$ f'''(x) = 2e^{2x} $$
And from the ( y ) part, we solve for ( g'(y) ): $$ -2f''(x) g'(y) = 3x^2y $$
- Solve for ( f(x) ) and ( g(y) )
-
Finding ( f(x) ): Integrate ( f'''(x) ): $$ f''(x) = \int 2e^{2x} dx = e^{2x} + C_1 $$ $$ f'(x) = \int (e^{2x} + C_1) dx = \frac{1}{2} e^{2x} + C_1 x + C_2 $$ $$ f(x) = \int \left(\frac{1}{2} e^{2x} + C_1 x + C_2\right) dx = \frac{1}{4} e^{2x} + \frac{C_1}{2} x^2 + C_2 x + C_3 $$
-
Finding ( g(y) ): Solve ( g'(y) ): $$ -2(g'(y)) = 3y \Rightarrow g'(y) = -\frac{3}{2}y $$ Integrate: $$ g(y) = \int -\frac{3}{2}y , dy = -\frac{3}{4}y^2 + C_4 $$
- Combine the Solutions
Combine the results for ( z(x, y) ): $$ z(x, y) = \frac{1}{4} e^{2x} + \frac{C_1}{2} x^2 + C_2 x + C_3 - \frac{3}{4}y^2 + C_4 $$
The general solution is: $$ z(x, y) = \frac{1}{4} e^{2x} + \frac{C_1}{2} x^2 + C_2 x - \frac{3}{4} y^2 + C_3 $$
More Information
This solution reflects a combination of both exponential and polynomial behaviors in the ( x ) and ( y ) dimensions. The constants ( C_i ) (where ( i = 1, 2, 3, 4 )) can be set based on initial or boundary conditions.
Tips
- Forgetting to differentiate correctly when taking higher order derivatives.
- Neglecting the constants of integration; they are essential in forming the general solution.
- Assuming ( g(y) ) must be zero; it can contain any constant term.
AI-generated content may contain errors. Please verify critical information