Solve \( \frac{d^2y}{dx^2} - 4 \frac{dy}{dx} + 3y = 0. \)
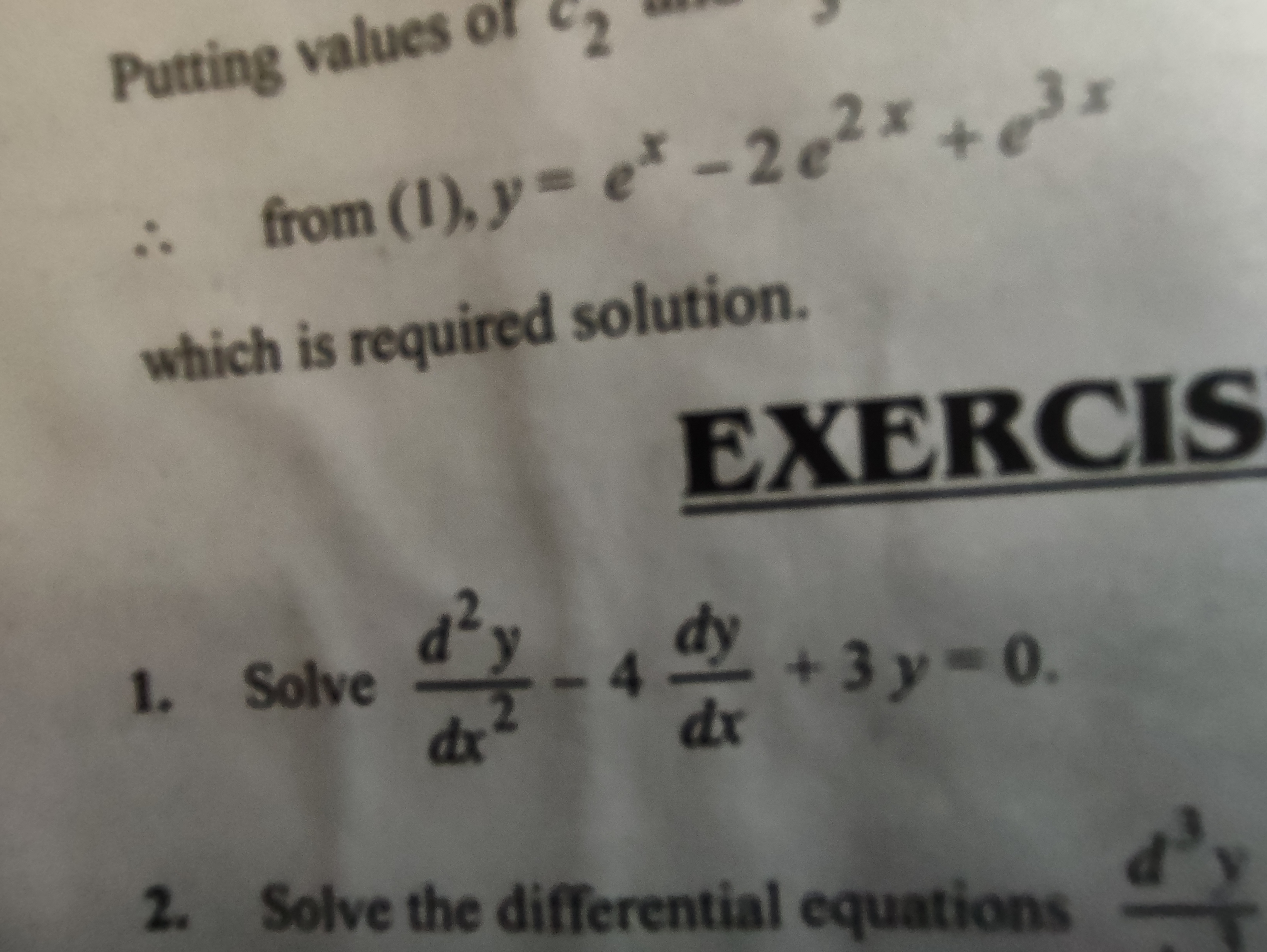
Understand the Problem
The question is asking to solve a second-order differential equation. This requires finding a function that satisfies the provided equation, which likely involves techniques for solving ordinary differential equations.
Answer
The general solution is: $$ y = c_1 e^x + c_2 e^{3x} $$
Answer for screen readers
The general solution to the given differential equation is:
$$ y = c_1 e^x + c_2 e^{3x} $$
Steps to Solve
-
Identify the differential equation
The equation given is a second-order linear homogeneous differential equation:
$$ \frac{d^2y}{dx^2} - 4 \frac{dy}{dx} + 3y = 0 $$ -
Find the characteristic equation
To solve this, we first assume a solution of the form $y = e^{rx}$.
Substituting this into the differential equation leads to the characteristic equation:
$$ r^2 - 4r + 3 = 0 $$ -
Solve the characteristic equation
We can factor the characteristic equation:
$$ (r - 1)(r - 3) = 0 $$
Thus, the roots are $r_1 = 1$ and $r_2 = 3$. -
Write the general solution
The general solution of the differential equation is formed using the roots:
$$ y = c_1 e^{1x} + c_2 e^{3x} $$
This can be simplified to:
$$ y = c_1 e^x + c_2 e^{3x} $$ -
Simplify the final solution
The constants $c_1$ and $c_2$ are determined based on initial conditions or boundary values if provided. As we are looking for a general form, we write the solution as:
$$ y = c_1 e^x + c_2 e^{3x} $$
The general solution to the given differential equation is:
$$ y = c_1 e^x + c_2 e^{3x} $$
More Information
This solution represents a family of functions where $c_1$ and $c_2$ are constants that would be determined if specific initial conditions were given. Such differential equations often arise in various fields, such as physics and engineering, to describe phenomena like motion or electricity.
Tips
- Forgetting to factor the characteristic equation correctly; ensure the roots are simplified properly.
- Not considering the general form of the solution; always remember to include arbitrary constants when necessary.
AI-generated content may contain errors. Please verify critical information