Solve for z: \frac{5}{3z} + 1 = 3 - \frac{2}{3z}
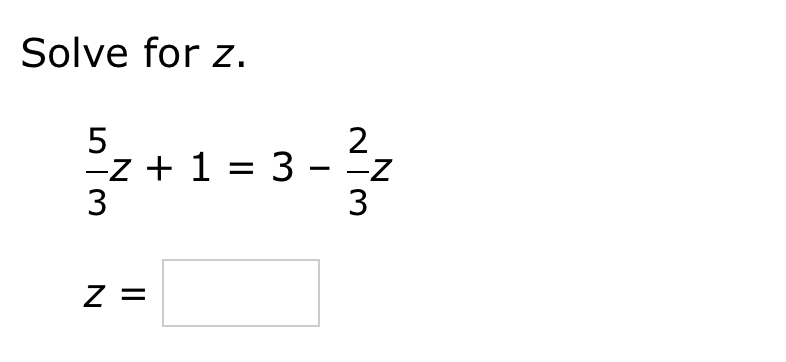
Understand the Problem
The question is asking to solve the equation for the variable z. This involves rearranging the given equation to isolate z on one side and find its value.
Answer
$$ z = \frac{7}{6} $$
Answer for screen readers
The final answer is:
$$ z = \frac{7}{6} $$
Steps to Solve
-
Isolate the fractions on one side First, let's eliminate the fractions by moving all terms involving $z$ to one side of the equation.
The equation is:
$$ \frac{5}{3z} + 1 = 3 - \frac{2}{3z} $$
Subtract $1$ from both sides:
$$ \frac{5}{3z} = 2 - \frac{2}{3z} $$ -
Combine the fractions Now, we’ll add $\frac{2}{3z}$ to both sides:
$$ \frac{5}{3z} + \frac{2}{3z} = 2 $$
This can be simplified into:
$$ \frac{7}{3z} = 2 $$ -
Cross-multiply to eliminate the fraction To solve for $z$, we can cross-multiply:
$$ 7 = 2 \cdot 3z $$
Which simplifies to:
$$ 7 = 6z $$ -
Solve for z Now, divide both sides by $6$:
$$ z = \frac{7}{6} $$
The final answer is:
$$ z = \frac{7}{6} $$
More Information
The solution indicates that $z$ is equal to $\frac{7}{6}$, which is an improper fraction. This solution may often arise in contexts involving rates or ratios in practical applications.
Tips
- Neglecting to combine fractions correctly: Ensure you bring like terms together properly.
- Incorrectly cross-multiplying: Focus on maintaining the order of the equation to avoid wrong results.
AI-generated content may contain errors. Please verify critical information