Solve for x: -9x + 3(x + 1) + 8 = -x - 10

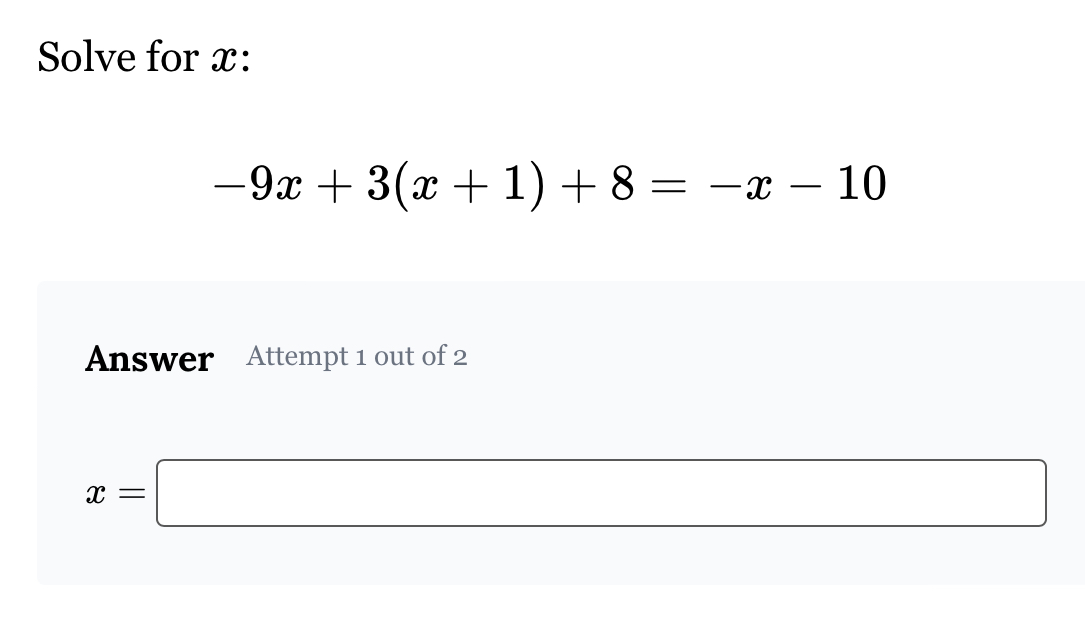
Understand the Problem

The question is asking to solve a linear equation for the variable x. The equation involves distributing, combining like terms, and isolating x to find its value.

Answer

$x = \frac{21}{5}$

Steps to Solve

Distribute the 3 in the equation

Start by expanding the term $3(x + 1)$: $$ 3(x + 1) = 3x + 3 $$ Substituting this back into the equation gives: $$ -9x + 3x + 3 + 8 = -x - 10 $$

Combine like terms on the left side

Combine the $-9x$ and $3x$ terms: $$ -6x + 11 = -x - 10 $$

Isolate the variable x

To isolate $x$, first add $x$ to both sides: $$ -6x + x + 11 = -10 $$ This simplifies to: $$ -5x + 11 = -10 $$

Subtract 11 from both sides

Now, subtract 11 from both sides to start isolating $x$: $$ -5x = -10 - 11 $$ This simplifies to: $$ -5x = -21 $$

Divide by -5

Finally, divide both sides by $-5$ to solve for $x$: $$ x = \frac{-21}{-5} = \frac{21}{5} $$

The value of $x$ is $x = \frac{21}{5}$.

More Information

The solution indicates that $x$ is equal to $\frac{21}{5}$, or 4.2 in decimal form. This demonstrates an application of algebraic techniques such as distribution, combining like terms, and isolating variables.

Tips

Not correctly distributing the $3$ in the term $3(x + 1)$.
Forgetting to combine like terms which can lead to an incorrect equation.
Misinterpreting signs when isolating $x$.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!