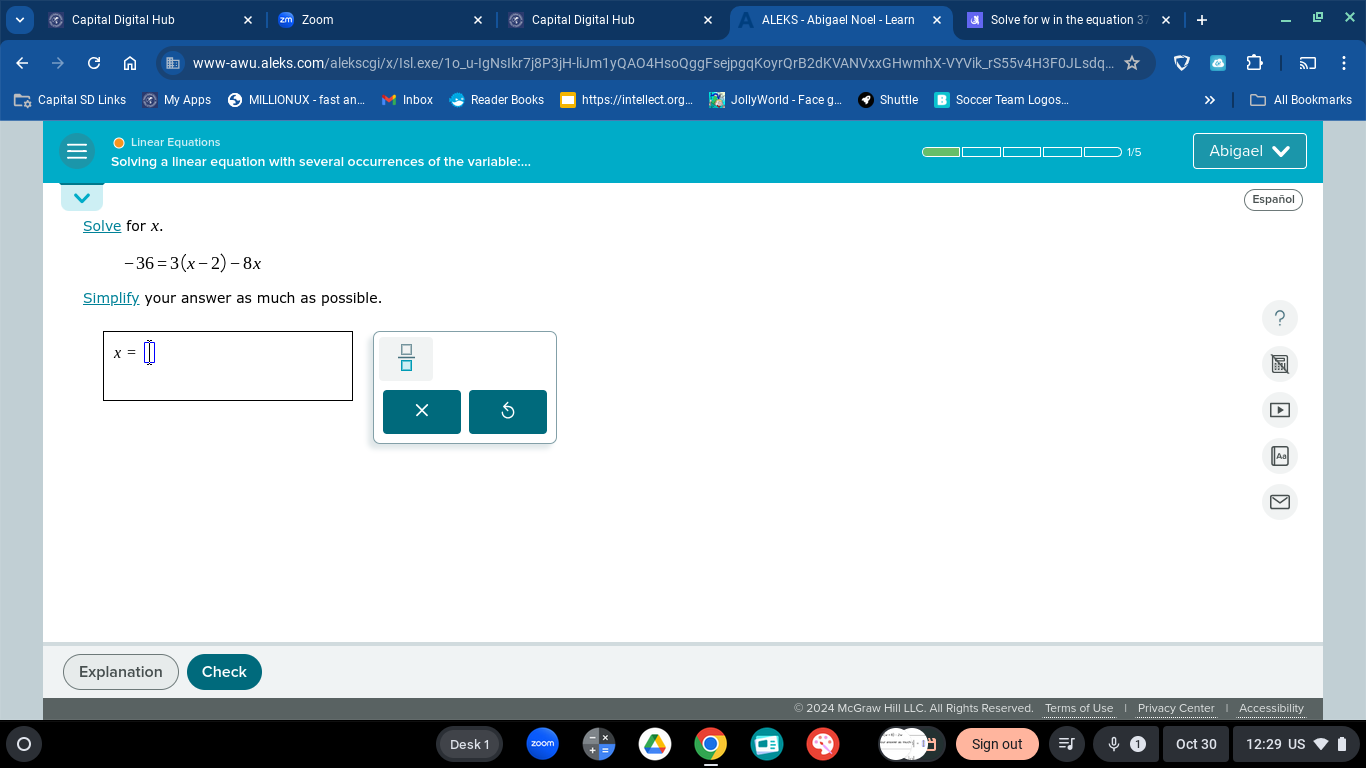
Solve for x: -36 = 3(x - 2) - 8x. Simplify your answer as much as possible.
Understand the Problem
The question is asking us to solve a linear equation for 'x', specifically the equation -36 = 3(x - 2) - 8x. It requires simplifying our answer as much as possible.
Answer
$x = 6$
Answer for screen readers
The solution for $x$ is $x = 6$.
Steps to Solve
- Distribute on the right side of the equation
Start with the equation: $$ -36 = 3(x - 2) - 8x $$
Distribute the $3$ into $(x - 2)$: $$ -36 = 3x - 6 - 8x $$
- Combine like terms
Combine $3x$ and $-8x$ on the right side: $$ -36 = (3x - 8x) - 6 $$
This simplifies to: $$ -36 = -5x - 6 $$
- Isolate the term with 'x'
Add $6$ to both sides to isolate the $-5x$: $$ -36 + 6 = -5x $$
This simplifies to: $$ -30 = -5x $$
- Solve for 'x'
Divide both sides by $-5$ to solve for $x$: $$ x = \frac{-30}{-5} $$
This simplifies to: $$ x = 6 $$
The solution for $x$ is $x = 6$.
More Information
This problem involved applying the distributive property and combining like terms. In linear equations like this, the goal is to isolate the variable on one side of the equation to find its value.
Tips
- Forgetting to distribute correctly when you first come across parentheses.
- Not combining like terms properly, which can lead to errors in the coefficients of the variables.
- Losing track of the negatives when adding or subtracting terms.
AI-generated content may contain errors. Please verify critical information