Solve the equations: 1) 3(2x - 14) - 3x = 13(x - 4) 2) -3x - 42 3) 3 = -9(x - 5) + 15x 4) -2.
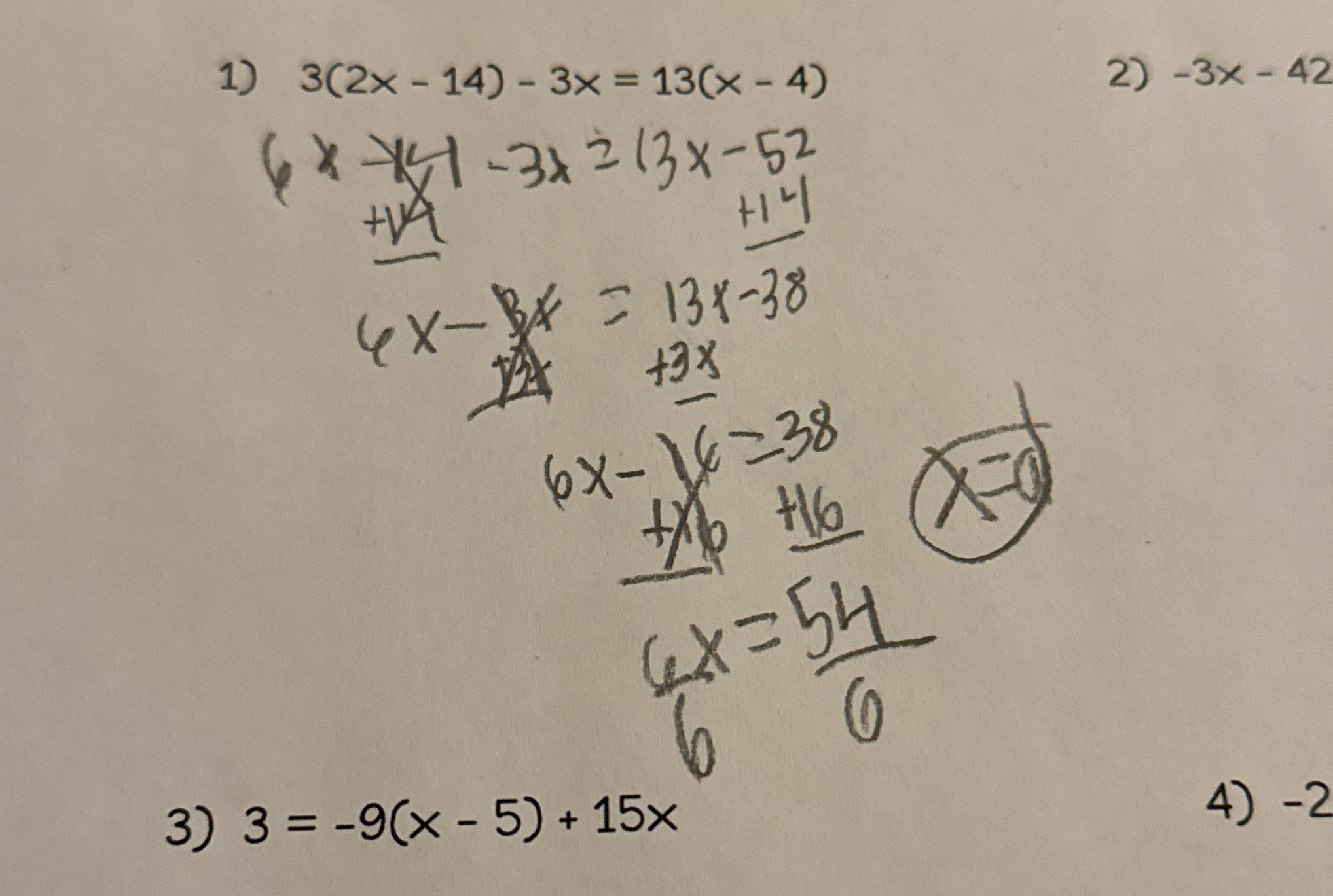
Understand the Problem
The question involves solving a set of algebraic equations. It appears that the user is working on simplifying and solving these equations for the variable x.
Answer
The solution is \( x = 1 \).
Answer for screen readers
The solution for the first equation is ( x = 1 ).
Steps to Solve
-
Expand the Equations Start with the first equation: $$ 3(2x - 14) - 3x = 13(x - 4) $$
Expanding both sides gives us: $$ 6x - 42 - 3x = 13x - 52 $$
-
Combine Like Terms Simplify the equation by combining like terms: $$ (6x - 3x) - 42 = 13x - 52 $$ which simplifies to: $$ 3x - 42 = 13x - 52 $$
-
Isolate Variables Next, isolate the variable $x$. Start by moving $13x$ to the left side: $$ 3x - 13x - 42 = -52 $$ This simplifies to: $$ -10x - 42 = -52 $$
-
Solve for $x$ Add 42 to both sides: $$ -10x = -10 $$ Then divide by -10: $$ x = 1 $$
-
Check the Solution Substitute $x = 1$ back into the original equation to confirm: $$ 3(2(1) - 14) - 3(1) = 13(1 - 4) $$ This simplifies to: $$ 3(-12) - 3 = 13(-3) $$ $$ -36 - 3 = -39 \rightarrow -39 = -39 \text{ (True)} $$
The solution for the first equation is ( x = 1 ).
More Information
The process of expanding, combining like terms, and isolating the variable is fundamental in solving algebraic equations. This example demonstrates how to manipulate and verify algebraic expressions properly.
Tips
- Mismanaging Signs: Be cautious with negative signs when moving terms across the equation.
- Failure to Check Solutions: Always verify the solution by substituting it back into the original equation to ensure accuracy.
AI-generated content may contain errors. Please verify critical information