Solve for t.
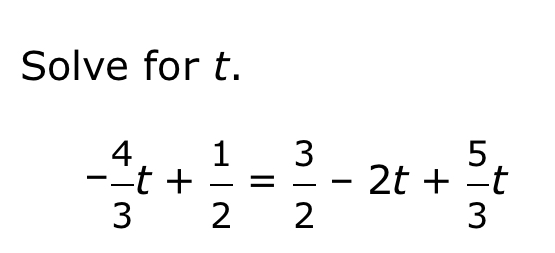
Understand the Problem
The question is asking to solve the equation given for the variable t. This involves isolating t on one side of the equation and performing algebraic manipulations to find its value.
Answer
$t = -1$
Answer for screen readers
The solution for $t$ is $t = -1$.
Steps to Solve
- Combine like terms on the right side
We start by combining the terms involving $t$ on the right side of the equation. The equation is given as: $$ \frac{-4}{3}t + \frac{1}{2} = \frac{3}{2} - 2t + \frac{5}{3}t $$
We can rewrite the right side: $$ -2t + \frac{5}{3}t = \left(-2 + \frac{5}{3}\right)t $$
Convert $-2$ to a fraction: $$ -2 = -\frac{6}{3} $$
Now combine the coefficients: $$ \left(-\frac{6}{3} + \frac{5}{3}\right)t = -\frac{1}{3}t $$
So the equation updates to: $$ \frac{-4}{3}t + \frac{1}{2} = \frac{3}{2} - \frac{1}{3}t $$
- Isolate the terms involving t
Next, we want to isolate the $t$ terms on one side. Let's first add $\frac{1}{3}t$ to both sides: $$ \frac{-4}{3}t + \frac{1}{3}t + \frac{1}{2} = \frac{3}{2} $$
Simplifying the left side gives: $$ \frac{-4 + 1}{3}t + \frac{1}{2} = \frac{3}{2} $$
This simplifies to: $$ \frac{-3}{3}t + \frac{1}{2} = \frac{3}{2} $$ So it becomes: $$ -t + \frac{1}{2} = \frac{3}{2} $$
- Solve for t
Now we need to isolate $t$. First, subtract $\frac{1}{2}$ from both sides: $$ -t = \frac{3}{2} - \frac{1}{2} $$
Calculate the right side: $$ -t = \frac{3 - 1}{2} = \frac{2}{2} = 1 $$
Now, multiply both sides by -1 to solve for $t$: $$ t = -1 $$
The solution for $t$ is $t = -1$.
More Information
This problem highlights the importance of combining like terms and isolating variables in linear equations. Understanding how to balance equations is crucial for solving algebraic expressions.
Tips
- Not combining like terms correctly, which can lead to confusion.
- Forgetting to distribute negative signs when moving terms across the equation.
- Not converting integers into fractions when necessary to combine terms.
AI-generated content may contain errors. Please verify critical information