Solve for m. 4 - 3/5 m = 6/5 m + 2
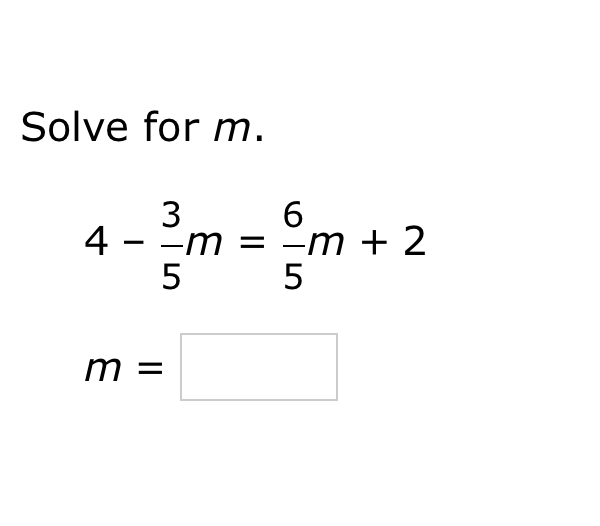
Understand the Problem
The question is asking to solve the equation for the variable m. The provided equation includes fractions and requires algebraic manipulation to isolate m on one side of the equation.
Answer
$$ m = \frac{10}{9} $$
Answer for screen readers
$$ m = \frac{10}{9} $$
Steps to Solve
- Isolate terms involving m on one side
We start with the equation: $$ 4 - \frac{3}{5} m = \frac{6}{5} m + 2 $$
Subtract $2$ from both sides: $$ 4 - 2 - \frac{3}{5} m = \frac{6}{5} m $$
This simplifies to: $$ 2 - \frac{3}{5} m = \frac{6}{5} m $$
- Combine like terms
Now, we add $\frac{3}{5} m$ to both sides: $$ 2 = \frac{6}{5} m + \frac{3}{5} m $$
This combines as: $$ 2 = \frac{9}{5} m $$
- Solve for m by isolating it
Next, we multiply both sides by the reciprocal of $\frac{9}{5}$, which is $\frac{5}{9}$: $$ m = 2 \times \frac{5}{9} $$
Calculating that gives: $$ m = \frac{10}{9} $$
$$ m = \frac{10}{9} $$
More Information
The final value of $m$ means that in this equation, the variable $m$ equals approximately 1.11. This solution can be useful in contexts where fractional values need to be understood or simplified in real-world scenarios.
Tips
- Not properly isolating $m$ on one side of the equation, leading to incorrect terms being manipulated.
- Miscalculating when adding or subtracting fractions.
- Forgetting to convert fractions properly when dealing with their reciprocals.
AI-generated content may contain errors. Please verify critical information