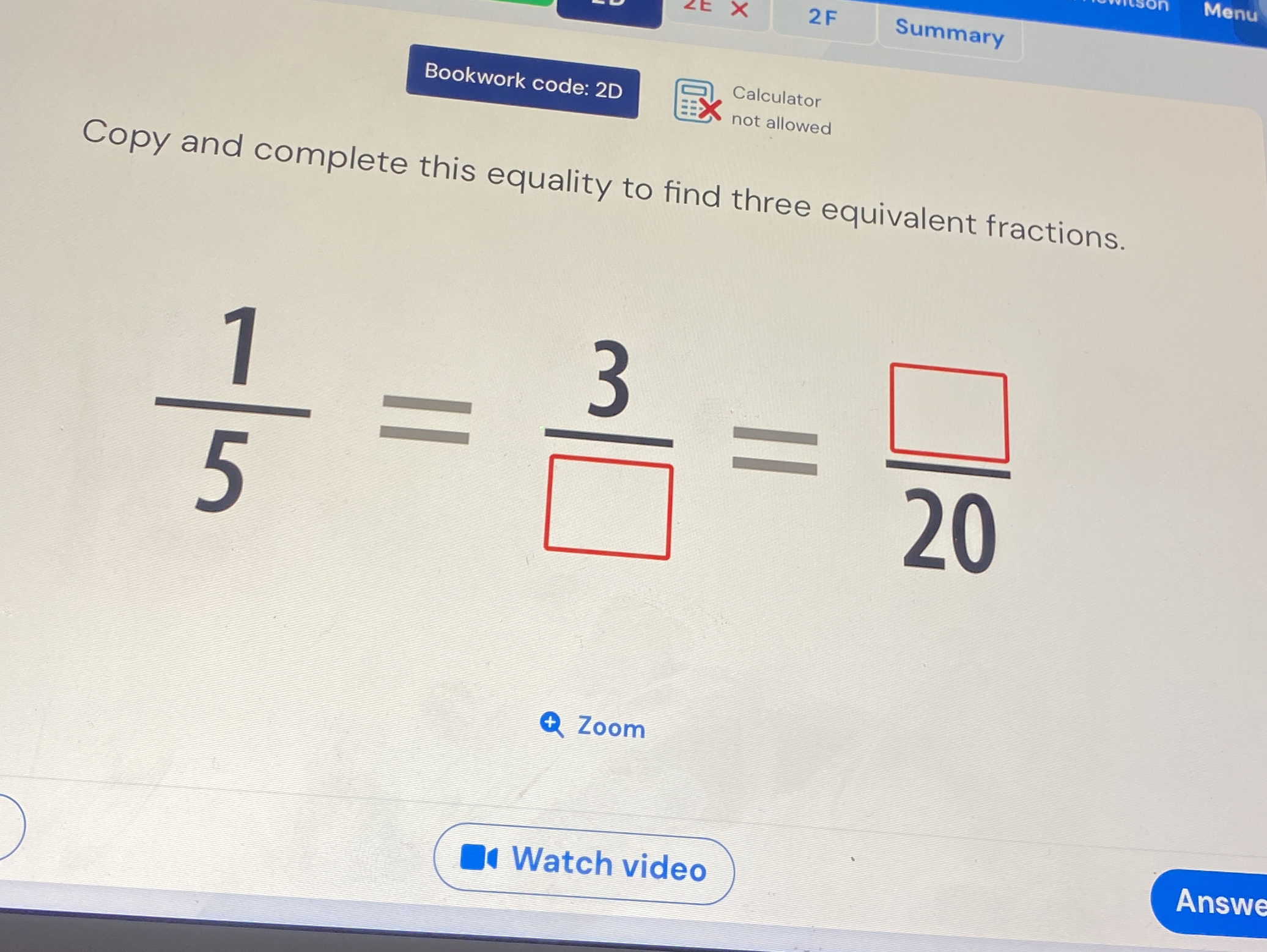
Copy and complete this equality to find three equivalent fractions.
Understand the Problem
The question is asking to find three equivalent fractions for the given fraction 1/5, and it shows partial equalities indicating that the answer must be filled in the blank spaces.
Answer
The three equivalent fractions for \( \frac{1}{5} \) are \( \frac{3}{15} \), \( \frac{4}{20} \), and \( \frac{5}{25} \).
Answer for screen readers
The three equivalent fractions for ( \frac{1}{5} ) are ( \frac{3}{15} ), ( \frac{4}{20} ), and ( \frac{5}{25} ).
Steps to Solve
- Understanding Equivalent Fractions
To find equivalent fractions, we can multiply the numerator and the denominator of the original fraction by the same non-zero number. For the fraction ( \frac{1}{5} ), we can choose different numbers to obtain equivalent fractions.
- Finding the First Equivalent Fraction
Let's multiply both the numerator (1) and the denominator (5) by 3: $$ \frac{1 \times 3}{5 \times 3} = \frac{3}{15} $$ This gives us ( \frac{3}{15} ) as one equivalent fraction.
- Finding the Second Equivalent Fraction
Next, we'll multiply both the numerator and the denominator by 4: $$ \frac{1 \times 4}{5 \times 4} = \frac{4}{20} $$ Now we have ( \frac{4}{20} ) as another equivalent fraction, which fills in the blank in the equation.
- Finding the Third Equivalent Fraction
Finally, we'll multiply both the numerator and the denominator by 5: $$ \frac{1 \times 5}{5 \times 5} = \frac{5}{25} $$ This gives us ( \frac{5}{25} ) as the last equivalent fraction.
The three equivalent fractions for ( \frac{1}{5} ) are ( \frac{3}{15} ), ( \frac{4}{20} ), and ( \frac{5}{25} ).
More Information
Equivalent fractions represent the same portion of a whole. They are created by multiplying both the numerator and denominator by the same number. This is a fundamental concept in understanding fractions.
Tips
Some common mistakes include:
- Forgetting to multiply both the numerator and the denominator by the same number, which will result in a different fraction.
- Assuming that one equivalent fraction is the only one possible, when in reality, multiple equivalent fractions can be formed.
AI-generated content may contain errors. Please verify critical information