Solve for f: \frac{2}{3}f - 3 = -1 + \frac{4}{9}f + \frac{4}{9}f + 6
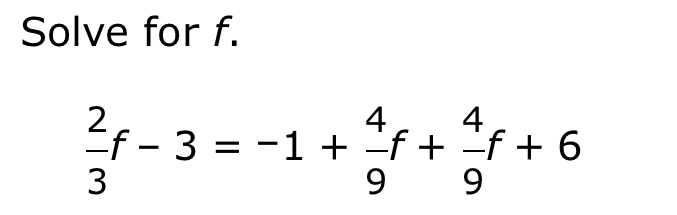
Understand the Problem
The question is asking to solve the equation for the variable f. This involves isolating f on one side of the equation and simplifying the equation step by step.
Answer
The value of $f$ is $-36$.
Answer for screen readers
The solution for $f$ is $f = -36$.
Steps to Solve
- Combine like terms on the right side
Start by simplifying the right-hand side of the equation: $$ -1 + 6 + \frac{4}{9}f + \frac{4}{9}f $$ This gives us: $$ 5 + \frac{8}{9}f $$
- Rewrite the equation
Now the equation looks like this: $$ \frac{2}{3}f - 3 = 5 + \frac{8}{9}f $$
- Isolate terms with f
Next, move all terms involving $f$ to one side and constant terms to the other side: $$ \frac{2}{3}f - \frac{8}{9}f = 5 + 3 $$
- Find a common denominator
To combine the $f$ terms, find a common denominator for $\frac{2}{3}$ and $\frac{8}{9}$. The common denominator is 9: $$ \frac{6}{9}f - \frac{8}{9}f = 8 $$
- Combine f terms
Now combine the $f$ terms: $$ -\frac{2}{9}f = 8 $$
- Solve for f
To isolate $f$, multiply both sides by -9/2: $$ f = 8 \times -\frac{9}{2} $$ Calculating this gives: $$ f = -36 $$
The solution for $f$ is $f = -36$.
More Information
This problem illustrates how to solve linear equations by isolating the variable. It also demonstrates the importance of combining like terms and keeping track of positive and negative signs.
Tips
- Forgetting to combine like terms correctly. Make sure to double-check each step to avoid errors.
- Not finding a common denominator when working with fractions. Always identify the least common multiple to simplify accurately.
AI-generated content may contain errors. Please verify critical information