Solve for c. 0.24 + 0.5c = -0.05 + 0.8c + 0.02
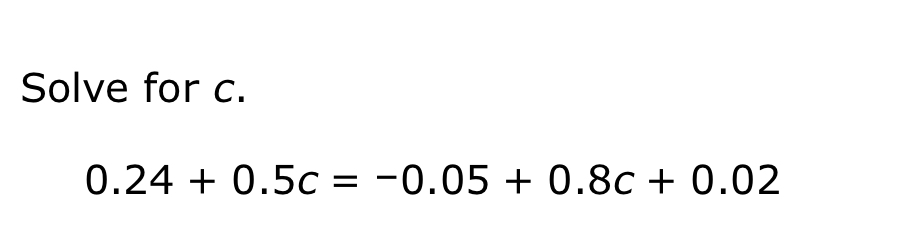
Understand the Problem
The question is asking to solve a linear equation for the variable c. This involves rearranging the equation to isolate c on one side. We need to combine like terms and perform algebraic steps to solve for c.
Answer
The solution is \( c = 0.9 \).
Answer for screen readers
The final answer is ( c = 0.9 ).
Steps to Solve
- Combine constants on both sides
On the right side, combine $-0.05$ and $0.02$: $$ -0.05 + 0.02 = -0.03 $$
So the equation is: $$ 0.24 + 0.5c = -0.03 + 0.8c $$
- Isolate c terms on one side
Move $0.5c$ from the left side to the right side by subtracting $0.5c$ from both sides: $$ 0.24 = -0.03 + 0.8c - 0.5c $$ This simplifies to: $$ 0.24 = -0.03 + 0.3c $$
- Combine like terms
Now we need to isolate $c$. First, add $0.03$ to both sides: $$ 0.24 + 0.03 = 0.3c $$ This simplifies to: $$ 0.27 = 0.3c $$
- Solve for c
To isolate $c$, divide both sides by $0.3$: $$ c = \frac{0.27}{0.3} $$
- Simplify the fraction
Perform the division: $$ c = 0.9 $$
The final answer is ( c = 0.9 ).
More Information
This equation is a simple linear equation in one variable. The process involved isolating the variable and simplifying, which is a fundamental skill in algebra.
Tips
- Forgetting to combine like terms before isolating the variable can lead to mistakes.
- Miscalculating when dividing decimals can also result in incorrect answers.
AI-generated content may contain errors. Please verify critical information