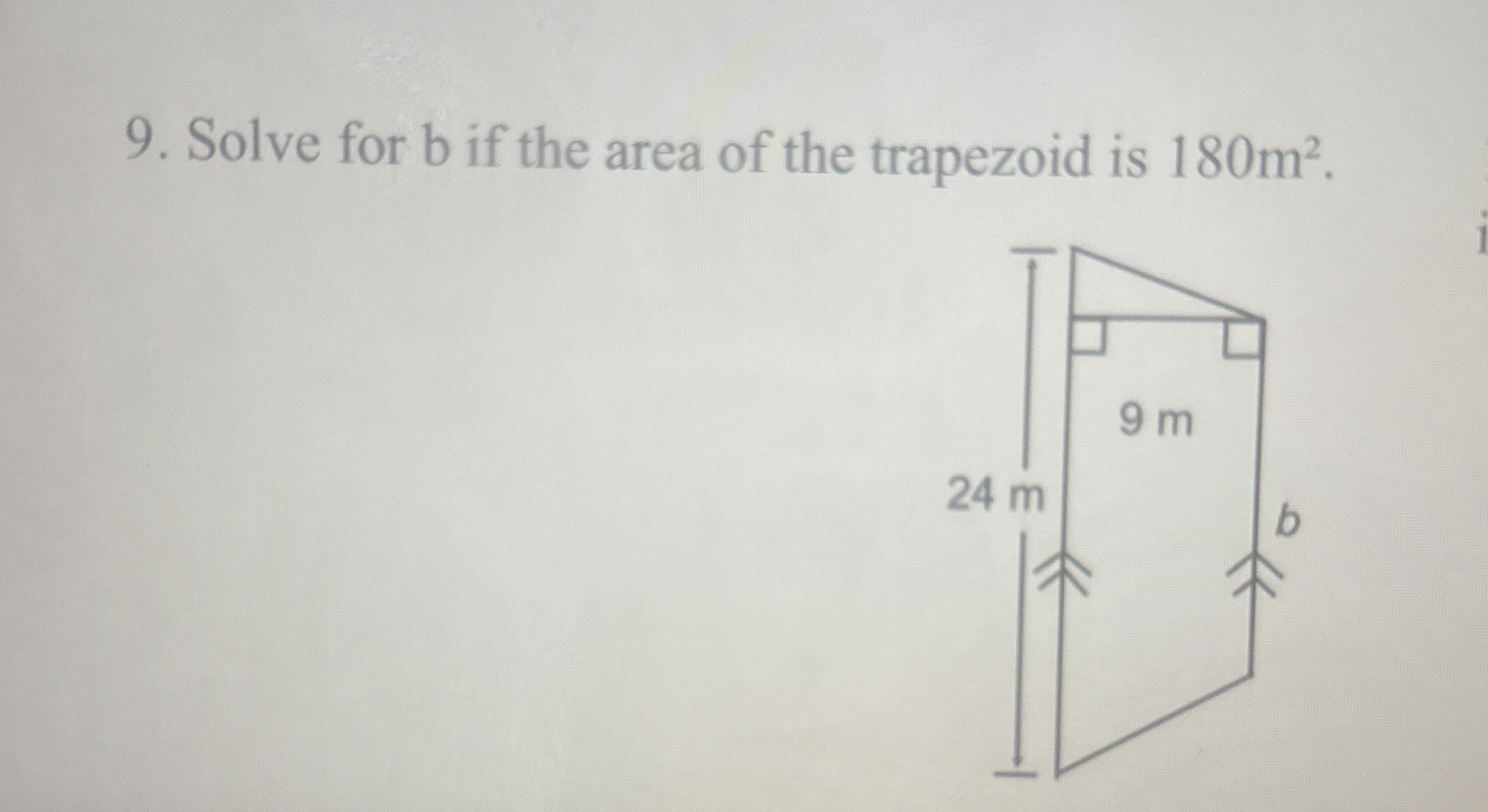
Solve for b if the area of the trapezoid is 180 m² and one base is 24 m and the other base is 9 m.
Understand the Problem
The question is asking to solve for the variable 'b' in a trapezoid when given the area and one of the base lengths. The area of a trapezoid is calculated using the formula A = (1/2) * (b1 + b2) * h, where b1 and b2 are the lengths of the two bases, and h is the height.
Answer
The length of the other base \( b \) is \( 16 \) m.
Answer for screen readers
The length of the other base ( b ) is 16 m.
Steps to Solve
- Identify the given information
The area ( A ) of the trapezoid is 180 m², one base ( b_1 = 24 ) m, and the height ( h = 9 ) m. We need to find the other base ( b_2 = b ).
- Use the area formula
The formula for the area of a trapezoid is
$$ A = \frac{1}{2} (b_1 + b_2) h $$
Substituting the known values:
$$ 180 = \frac{1}{2} (24 + b) \cdot 9 $$
- Simplify the equation
To simplify, multiply both sides by 2 to eliminate the fraction:
$$ 360 = (24 + b) \cdot 9 $$
Next, divide both sides by 9:
$$ 40 = 24 + b $$
- Solve for ( b )
Subtract 24 from both sides:
$$ b = 40 - 24 $$
So,
$$ b = 16 $$
The length of the other base ( b ) is 16 m.
More Information
The area of a trapezoid can vary depending on the lengths of the bases and the height. In this problem, we learned how to manipulate the area formula to solve for an unknown base length given the other parameters.
Tips
- Forgetting to multiply the area by 2 can lead to incorrect results.
- Not correctly distributing or simplifying fractions and equations may result in errors.
AI-generated content may contain errors. Please verify critical information