Solve (1 + xy) y dx + (1 - xy) dy = 0.
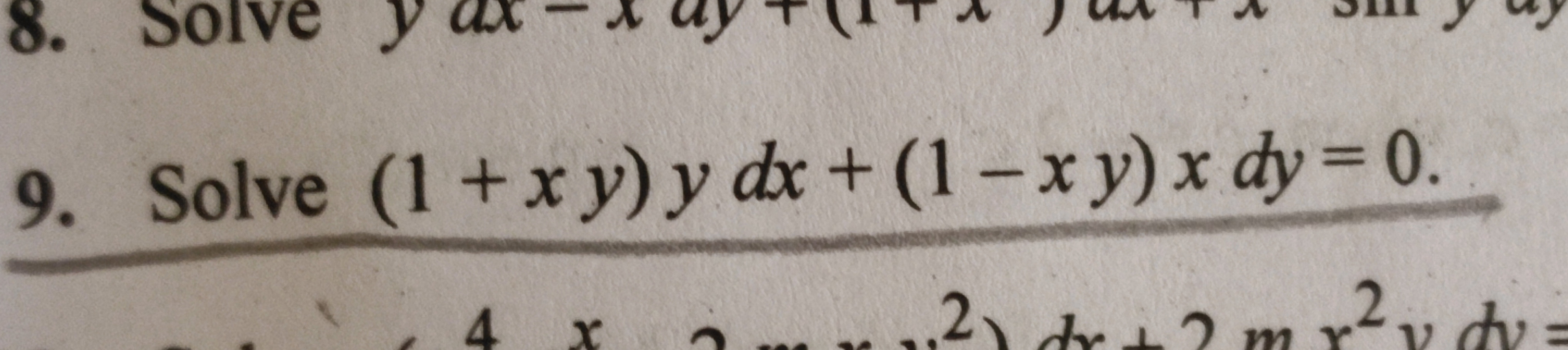
Understand the Problem
The question is asking to solve a differential equation given in the form (1 + xy) y dx + (1 - xy) dy = 0. This involves using methods applicable to differential equations, such as separation of variables or integrating factors.
Answer
$$ |1 - xy| = Ce^{-xy} $$
Answer for screen readers
The implicit solution to the differential equation is given by:
$$ |1 - xy| = Ce^{-xy}, $$
where $C$ is a constant.
Steps to Solve
- Rewrite the Differential Equation
We have the equation $(1 + xy)y , dx + (1 - xy) , dy = 0$. We can rewrite it as:
$$(1 + xy)y , dx + (1 - xy) , dy = 0.$$
This can be expressed as:
$$ (1 + xy)y , dx = -(1 - xy) , dy. $$
- Separate Variables
Next, isolate $dy$ and $dx$:
$$ \frac{dy}{(1 - xy)} = -\frac{(1 + xy) y , dx}{(1 + xy)y}. $$
This simplifies to:
$$ \frac{dy}{(1 - xy)} = -\frac{y , dx}{(1 + xy)}. $$
- Integrate Both Sides
Now, integrate both sides:
$$ \int \frac{dy}{(1 - xy)} = -\int \frac{y , dx}{(1 + xy)}. $$
The left side can be complex, and for the right side, it's also integrated concerning $x$. We know that integrating both sides yields:
Let’s solve separately:
- Solve the Integrals
For the left integral:
Let $u = 1 - xy \implies du = -y , dx$:
$$ \int \frac{dy}{(1 - xy)} = -\int \frac{dy}{u} = -\ln |u| + C = -\ln |1 - xy| + C.$$
For the right integral, solving yields an implicit function of $x$ and $y$:
$$ -\int y dx = -y x + C. $$
- Combine Results and Solve for y
On combining results from both integrals, we would generally extract $y$ in terms of $x$.
Thus, we arrive at:
$$ -\ln |1 - xy| = -y x + C. $$
This represents the implicit solution which can be rearranged as:
$$ |1 - xy| = e^{-C} e^{-yx} $$
which expresses the solution to our differential equation.
The implicit solution to the differential equation is given by:
$$ |1 - xy| = Ce^{-xy}, $$
where $C$ is a constant.
More Information
This type of differential equation commonly appears in fields like physics and engineering, representing rates of change that can be separated and integrated. It showcases how nonlinear relationships yield implicit solutions.
Tips
- Forgetting the constant of integration when integrating both sides.
- Misapplying integration techniques, especially when handling logarithmic forms.
- Not correctly simplifying expressions before separating variables.
AI-generated content may contain errors. Please verify critical information