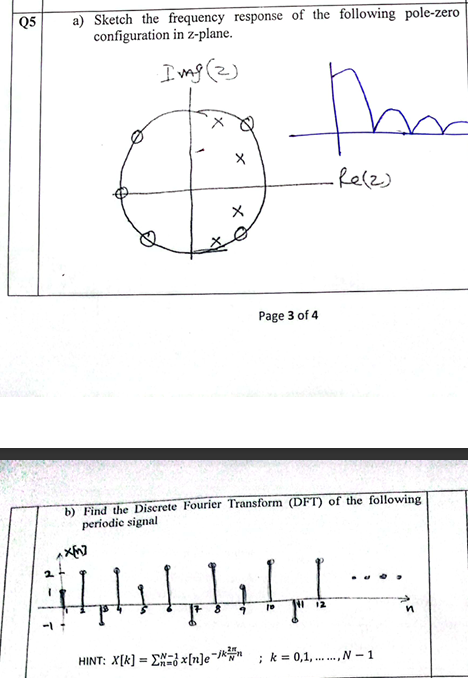
Sketch the frequency response of the following pole-zero configuration in z-plane. Find the Discrete Fourier Transform (DFT) of the following periodic signal.

Steps to Solve

1. Sketch the Frequency Response

   To sketch the frequency response, identify the zeros (denoted by "o") and poles (denoted by "x") on the unit circle in the z-plane. The poles and zeros affect the frequency response significantly. The frequency response can often be visualized by substituting $z = e^{j\omega}$ where $\omega$ is the frequency.

2. Determine the Magnitude and Phase

   Calculate the magnitude $|H(e^{j\omega})|$ and phase $\angle H(e^{j\omega})$ for the given configuration by evaluating the transfer function at different values of $\omega$. The formula for the frequency response is given by:

   $$ H(e^{j\omega}) = \frac{Z(e^{j\omega})}{P(e^{j\omega})} $$

   where $Z(e^{j\omega})$ is the product of the zeros and $P(e^{j\omega})$ is the product of the poles.

3. Analyze the Plot

   Based on the zero and pole configuration, plot the magnitude and phase response on the Cartesian plane where the x-axis represents $\omega$ and the y-axis represents the magnitude and phase.

4. Finding the DFT of a Periodic Signal

   The Discrete Fourier Transform (DFT) is defined as:

   $$ X[k] = \sum_{n=0}^{N-1} x[n] e^{-j\frac{2\pi}{N}kn} $$

   where $N$ is the number of samples and $k$ is the frequency index ranging from $0$ to $N-1$.

5. Apply the DFT to the Given Signal

   Using the provided periodic signal, plug in the values for $x[n]$ and compute $X[k]$ for each value of $k$. Make sure to account for how many total samples $N$ there are, and adjust the equations accordingly.

6. Document the Results

   Once both parts are computed and plotted, ensure the results are neatly documented, along with any notable observations regarding frequency components identified in the DFT.