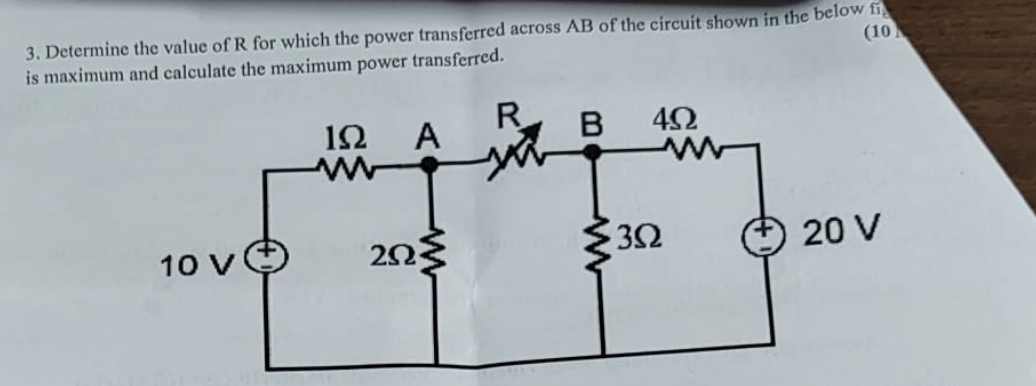
Determine the value of R for which the power transferred across AB of the circuit shown in the below figure is maximum and calculate the maximum power transferred.

Steps to Solve

1. Identifying the Effective Resistance for Maximum Power Transfer To achieve maximum power transfer, the resistance $R$ must equal the Thevenin equivalent resistance ($R_{th}$) seen from the terminals A and B. We will first calculate $R_{th}$.

2. Finding the Thevenin Resistance To find $R_{th}$, we deactivate the independent voltage sources (replace 10V and 20V with short circuits) and find the equivalent resistance seen from terminals A and B.

   The combination of resistors is as follows:

   • The $2 , \Omega$ and $3 , \Omega$ resistors are in series.
   • The equivalent resistance of $2 , \Omega$ and $3 , \Omega$ in series is: $$ R_{2,3} = 2, \Omega + 3, \Omega = 5, \Omega $$
   • This $5 , \Omega$ is in parallel with the $4 , \Omega$ resistor: $$ R_{th} = \frac{R_{2,3} \cdot 4 , \Omega}{R_{2,3} + 4 , \Omega} = \frac{5 \cdot 4}{5 + 4} = \frac{20}{9} \approx 2.22, \Omega $$

3. Setting Up for Maximum Power Transfer For maximum power transfer, the resistance $R$ must equal $R_{th}$: $$ R = R_{th} \approx 2.22 , \Omega $$

4. Calculating Maximum Power Transferred Now, we find the maximum power transferred using the formula: $$ P_{max} = \frac{V_{th}^2}{4R_{th}} $$ We need to determine the Thevenin voltage ($V_{th}$) at terminals A and B with the independent sources active.

5. Calculating Thevenin Voltage The voltage across terminals A and B can be calculated using voltage division.

• The voltage seen at A can be found using the voltage divider: $$ V_{th} = 10V \cdot \frac{4, \Omega}{4, \Omega + 3, \Omega} = 10V \cdot \frac{4}{7} \approx 5.71 , V $$

6. Calculating Maximum Power Substituting into the power equation: $$ P_{max} = \frac{(5.71)^2}{4 \cdot (2.22)} \approx \frac{32.55}{8.88} \approx 3.66 , W $$