sin 3x
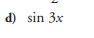
Understand the Problem
The question appears to be referencing a function related to trigonometry, specifically the sine function evaluated at 3x. The context is likely part of a larger problem involving trigonometric functions.
Answer
The function is $y = \sin(3x)$ with a period of $\frac{2\pi}{3}$.
Answer for screen readers
The function is $y = \sin(3x)$ with a period of $\frac{2\pi}{3}$.
Steps to Solve
-
Identify the function The function given is $y = \sin(3x)$. This indicates we are dealing with a sine wave that has been altered by a factor of 3.
-
Understand the effect of the coefficient The coefficient 3 before $x$ in the sine function compresses the wave horizontally. Specifically, it affects the period of the sine function, which is calculated using the formula: $$ \text{Period} = \frac{2\pi}{|k|} $$ where $k$ is the coefficient of $x$. Here, $k = 3$.
-
Calculate the period Using the formula mentioned: $$ \text{Period} = \frac{2\pi}{3} $$ Thus, the sine function $\sin(3x)$ completes one full cycle every $ \frac{2\pi}{3} $ units along the x-axis.
-
Graph the function (optional) If graphing, start at the origin (0,0). The sine function reaches its maximum of 1 at $x = \frac{\pi}{6}$, returns to 0 at $x = \frac{\pi}{3}$, reaches its minimum of -1 at $x = \frac{\pi}{2}$, and repeats this pattern every $\frac{2\pi}{3}$.
The function is $y = \sin(3x)$ with a period of $\frac{2\pi}{3}$.
More Information
This function represents a sine wave that oscillates between -1 and 1 with a quicker frequency due to the multiplication by 3, resulting in more cycles over the same interval compared to the standard sine function.
Tips
- Misunderstanding the period: A common mistake is incorrectly calculating the period. Remember to use the formula $ \frac{2\pi}{|k|} $ correctly.
- Graphing incorrectly: Not accounting for the compressing effect can lead to inaccurate graphs. Ensure the peaks and troughs are adjusted according to the new period.
AI-generated content may contain errors. Please verify critical information